Zad. 1. Przez dowolny punkt D na boku AC trójkąta ABC poprowadzono proste równoległe do środkowych AE i CF, przecinające boki AB i BC odpowiednio w punktach H i G. Wykaż, że środkowe AE i CF dzielą odcinek HG na trzy równe części.
Zad. 2. Dany jest trójkąt ABC. Znajdź zbiór punktów M takich, że trójkąty AMB i AMC mają równe pola.
Zad. 3. Wykaż, że jeśli w sześciokącie ABCDEF przeciwległe boki (tzn. AB i DE, AF i CD, EF i BC) są równoległe, a główne przekątne AD, BE i CF są równej długości, to można na nim opisać okrąg.
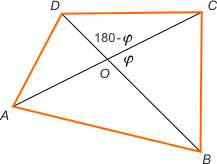
Zad. 4. (wolna amerykanka) Przekątne czworokąta ABCD przecinają się w punkcie O. Znajdź pole czworokąta, jeśli pola trójkątów ABD, ACD i AOD wynoszą odpowiednio a, b i c.
Za rozwiązania zadań 1-3 punkty zdobyli:
- 30 - Tadeusz Porzucek (emerytowany nauczyciel, Gostyń)
- 28 - Robert Ciężabka (student AGH Kraków), Michel Migas (student PW),
- 22 - Szymon Kaźmierowski (nauczyciel, IV LO Elbląg), Paweł Wesołowski (uczeń II LO Końskie),
- 20 - Sabina Khady Sy (studentka nanotechnologii na UJ),
- 12 - Mikołaj Sikora (uczeń III LO Tarnów).
Za zadanie 4 maksymalną liczbę 10 pkt. otrzymali: Robert Ciężabka, Zygmunt Krawczyk (nauczyciel, SLO Żary), Michel Migas, Tadeusz Porzucek, Mikołaj Sikora, Sabina Khady Sy, Szymon Kaźmierowski oraz Wojciech Tomiczek (inżynier, Lipowa).
Po 9 miesiącach trwania kolejnej edycji Ligi z Geometrii Elementarnej wyniki czołówki są następujące (na 270 możliwych punktów):
- 268 pkt. - Robert Ciężabka, Michel Migas, Tadeusz Porzucek
- 240 pkt. - Paweł Wesołowski
- 222 pkt. - Mikołaj Sikora
- 168 pkt. - Sabina Khady Sy
- 142 pkt. - Szymon Kaźmierowski
- 120 pkt. - Jacek Bagiński
Pozostali zawodnicy uzyskali wyniki poniżej 90 pkt.
W konkurencji wolnej amerykanki najwyżej w klasyfikacji znaleźli się:
- 90 pkt. (na 90 możliwych!) - Zygmunt Krawczyk, Michel Migas, Tadeusz Porzucek, Mikołaj Sikora i Robert Ciężabka,
- 88 pkt. - Sabina Khady Sy,
- 82 pkt. - Wojciech Tomiczek,
- 50 pkt. - Szymon Kaźmierowski.
Pozostali zawodnicy uzyskali poniżej 50 pkt.
Zad. 1. Z podobieństwa trójkątów CDG i CAE (cecha kkk) otrzymujemy |DG|/|CG| = |AE|/|EC|, a z podobieństwa trójkątów CPG i CME mamy |PG|/|CG| = |ME|/|EC|. Dzieląc stronami pierwszą z tych równości przez drugą, otrzymujemy |PG|/|DG| = |ME|/|AE| = 1/3, bo M jest środkiem ciężkości trójkąta ABC. Z kolei z podobieństwa trójkątów DHG i PKG (cecha kkk) mamy |KG|/|HG| = |PG|/|DG| = 1/3, skąd |KG| = |HG|/3. Analogicznie |HL| = |HG|/3. Stąd teza.
Zad. 2. Niech M będzie szukanym punktem.
a) Niech B i C leżą po obu stronach prostej AM. Oznaczmy przez S punkt wspólny prostej AM i boku BC. Trójkąty ABM i AMC mają równe pola oraz wspólną podstawę, więc ich wysokości CE i BF mają równe długości. Oznacza to, że trójkąty prostokątne CES i SFB są przystające (cecha kbk). Stąd S jest środkiem boku BS. I na odwrót: gdy S jest środkiem boku BC, to z przystawania trójkątów CES i SFB wynika równość pól trójkątów ABM i AMC.
b) Niech B i C leżą po jednej stronie prostej AM. Z założenia otrzymujemy równość wysokości CE i BF, skąd wynika równoległość prostej AM i boku BC. I na odwrót, jeśli prosta AM jest równoległa do BC, to trójkąty AMB i AMC mają równe pole, bo mają wspólną podstawę i równe wysokości.
Szukanym zbiorem są więc dwie proste przechodzące przez wierzchołek A z jego wyłączeniem. Pierwsza z nich przechodzi przez środek boku BC, a druga jest do tego boku równoległa.
Zad. 3. W świetle założeń trapezy ABCD, BCEF i ACDF są równoramienne. Otrzymujemy następujące równości miar kątów: |∡BAD|=|∡ADE|=|∡ABE|=|∡BED|, |∡ADC|=|∡FAD|=|∡DCF|=|∡FAD| oraz |∡FED|=|∡EBC|=|∡BCF|=|∡CFE|.
Rozważmy czworokąt FCDE. Mamy |∡EFC|+|∡EDA|+|∡ADC| = |∡FCD|+|∡FEB|+|∡BED|. To oznacza, że na tym czworokącie można opisać okrąg. Wobec równości |∡FDE|=|∡FBE| okrąg ten przechodzi także przez wierzchołek B. Analogicznie wobec równości |∡BAD|=|∡BED| okrąg ten przechodzi przez A. Stąd teza.
Zad. 4. (wolna amerykanka) Oznaczmy przez x pole trójkąta BOC. Otrzymujemy PΔAOD / PΔODC = |AO|/|OC| = PΔABO / PΔBOC. Podstawiając dane, otrzymujemy równanie c/b-c = a-c/x, skąd x = (a-c)(b-c)/c. Pole czworokąta ABCD jest sumą pól poszczególnych trójkątów i wynosi ab/c.
Czy wiesz, kto z wrocławskich matematyków został uwiecz-niony na tym znakomitym portrecie w piżamie? Kto jest autorem tego obrazu? Gdzie można go obejrzeć?
Jako młody chłopak Knaster ożenił się z poznaną w Paryżu Marią Morską - muzą Skaman-drytów (zm. w 1945 roku). W czasach wrocła-wskich jego drugą żoną była Regina Lewandowska. Pierwszej żonie Knastera poświęcona jest książka Hanny Faryny-Paszkiewicz "Opium życia".
Steinhaus twierdził, że nazwisko Knaster brzmi w dopeł-niaczu Knastra, a sam Knaster upierał się przy formie Knastera. 
