Zad. 1. Okręgi o promieniach 3 i 4 przecinają się w punktach A i B. Odległość ich środków wynosi 5. Przez punkt B poprowadzono prostą przecinającą okręgi w punktach C i D, przy czym |CD| = 8 i punkt B leży między C i D. Oblicz pole trójkąta ACD.
Zad. 2. Okręgi s1 i s2 przecinają się w punktach A i B, przy czym środek O okręgu s1 leży na okręgu s2. Cięciwa AC okręgu s1 przecina okrąg s2 w punkcie D. Wykaż, że odcinki OD i BC są prostopadłe.
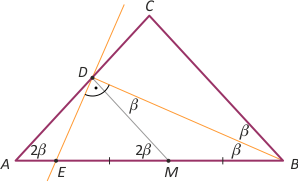
Zad. 3. W trójkącie równoramiennym ABC o podstawie AB poprowadzono dwusieczną BD, (D leży na AC). Prosta przechodząca przez D i prostopadła do BD przecina bok AB w punkcie E. Wykaż, że |EB| = 2|AD|.
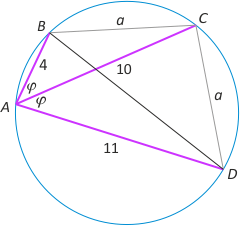
Zad. 4. (wolna amerykanka) W okręgu dane są cięciwy o długościach |AB|=4, |AC|=10 i |AD|=11, przy czym AC leży na dwusiecznej kąta DAB. Oblicz promień okręgu.
Za zadania 1-3 punkty otrzymali:
- 30 - Jacek Bagiński (nauczyciel matematyki, Kraków), Dominik Bysiewicz (student UJ), Tadeusz Porzucek (emerytowany nauczyciel, Gostyń), Iwona Gruszecka (nauczyciel matematyki, Warszawa), Elżbieta Grzechnik (emerytowany nauczyciel, Radom), Mikołaj Popek (student UAM) i Janusz Wieczorek (emerytowany nauczyciel, Sandomierz),
- 12 - Krzysztof Konarski (emerytowany nauczyciel, Poznań).
Za zadanie 4 punkty otrzymali:
- 10 pkt - Jacek Bagiński, Elżbieta Grzechnik, Krzysztof Konarski, Janusz Wieczorek, Mikołaj Popek i Tadeusz Porzucek,
- 8 pkt - Dominik Bysiewicz.
Gratulujemy!
Z przyjemnością informujmy, że uczestnicy Ligi: Dominik Bysiewicz i Tadeusz Porzucek bardzo udanie wystartowali w tegorocznej edycji Mistrzostw Polski w Geometrii Elementarnej (Dominik Bysiewicz zdobył II miejsce). Gratulacje!
Zad. 1. Zauważmy, że |∡DCA| = |∡BO1A|/2 = α oraz |∡CDA| = |∡AO2B|/2 = β, a stąd trójkąty ACD i O1O2A są podobne w skali k = |CD|:|O1O2| = 8/5. Trójkąt O1O2A jest prostokątny na mocy twierdzenia odwrotnego do twierdzenia Pitagorasa, zatem SACD = k2·SO1O2A = (64/25)·6 = 384/25.
Zad. 2. a) Niech okrąg S1 ma mniejszy promień. Zauważmy, że kąty ADO i ODB mają równe miary jako wpisane w okrąg i oparte na przystających cięciwach. Czworokąt AOBD jest wpisany w okrąg, więc |∡CAB| = |∡OBD| = β, a |∡ACO| = β, bo trójkąt COA jest równoramienny. Oznacza to, że trójkąty COD i DOB są przystające (z cechy kbk) i |DC| = |DB|. Ponadto |OC| = |OB|, zatem odcinek OD zawiera się w symetralnej odcinka BC, a stąd wynika teza.
b) Niech teraz S1 ma większy promień. Łatwo zauważyć, że kąty DOB i DAB mają równe miary (jako wpisane w okrąg i oparte na cięciwie DB), a z drugiej strony kąt COB (jako środkowy w okręgu S1) jest dwa razy większy od kąta DOB. Oznacza to, że odcinek OD zawiera się w dwusiecznej kąta w trójkącie równoramiennym COB, jest więc jednocześnie prostopadły do podstawy CB. Inne przypadki położenia punktu D analizujemy analogicznie.
Zad. 3. Niech M będzie środkiem odcinka EB. Wówczas środkowa DM w trójkącie prostokątnym EDB dzieli go na dwa trójkąty równoramienne przy czym |∡MDB| = |∡MBD| = β. Wówczas |∡EMD| = 2β, jako kąt zewnętrzny trójkąta, zatem trójkąt AMD jest równoramienny i |AD| = |DM|. Z własności środkowej przeciwprostokątnej dostajemy tezę.
Zad. 4. (wolna amerykanka) Wprowadźmy oznaczenia jak na rysunku. Zachodzi |BC| = |CD| = a, bo oparte na tych cięciwach kąty są przystające. Z twierdzenia Ptolomeusza dla czworokąta ABCD mamy 11·a + 4·a = 10·|BD|, skąd |BD| = 3a/2. Z twierdzenia kosinusów w trójkącie BDC mamy (9/4)·a2 = 2·a2–2·a2cos|∡BCD|, skąd cos|∡BCD| = -(1/8). Zauważmy teraz, że |∡BAD| = 180°–|∡BCD|, czyli cos|∡BAD| = 1/8. Dalej z "jedynki trygonometrycznej" mamy sin|∡BAD| = √63/8, a z twierdzenia kosinusów w trójkącie ABD mamy |BD| = 3√14. Ostatecznie z twierdzenia sinusów w trójkącie ABD otrzymujemy 2R = |BD|/sin|∡BAD|, skąd R = 4√2.
Czy wiesz, kto z wrocławskich matematyków został uwiecz-niony na tym znakomitym portrecie w piżamie? Kto jest autorem tego obrazu? Gdzie można go obejrzeć?
Jako młody chłopak Knaster ożenił się z poznaną w Paryżu Marią Morską - muzą Skaman-drytów (zm. w 1945 roku). W czasach wrocła-wskich jego drugą żoną była Regina Lewandowska. Pierwszej żonie Knastera poświęcona jest książka Hanny Faryny-Paszkiewicz "Opium życia".
Steinhaus twierdził, że nazwisko Knaster brzmi w dopeł-niaczu Knastra, a sam Knaster upierał się przy formie Knastera. 
