Zad. 1. W trójkącie ABC zachodzi: |AC|=40, |BC|=25, a kąt A jest dwa razy mniejszy od kąta B. Oblicz pole tego trójkąta.
Zad. 2. W trójkącie ABC punkt M jest środkiem boku AB, |∡MCB|=15°, a |∡AMC|=45°. Znajdź miarę kąta ACM.
Zad. 3. Przez ortocentrum H trójkąta ABC prowadzimy styczne do okręgów opisanych na trójkątach CHB i AHB. Przecinają one prostą AC odpowiednio w punktach K i L. Wykaż, że trójkąt KLH jest równoramienny.
Zad. 4. (wolna amerykanka) W trójkącie ABC punkt D jest spodkiem wysokości opuszczonej na przeciwprostokątną AB, a jednocześnie jest wierzchołkiem trójkąta KDL wpisanego w trójkąt ABC tak, że K leży na boku AC, L leży na boku BC, kąt KDL jest prosty, |KC|=5, |AK|=10 i |DB|=16. Oblicz pole trójkąta KDL.
Za zadania 1-3 komplet 30 punktów otrzymali: Dominik Bysiewicz (student matematyki na UJ), Elżbieta Grzechnik (emerytowana nauczycielka z Radomia), Sławomir Matysiak (nauczyciel, X LO Wrocław), Mikołaj Popek (student UAM), Tadeusz Porzucek (emerytowany nauczyciel z Gostynia), Radosław Górzyński (uczeń, I LO Lubin) oraz Krzysztof Konarski (emerytowany nauczyciel z Poznania).
Za zadanie 4 po 10 punktów otrzymali: Dominik Bysiewicz, Elżbieta Grzechnik, Mikołaj Popek, Tadeusz Porzucek oraz Zygmunt Krawczyk (emerytowany nauczyciel ze Szprotawy).
Gratulujemy!
Zad. 1. Niech D będzie takim punktem na boku AB, że |∡CDB|=2α. Kąt CDB jest zewnętrzny w trójkącie ADC stąd |∡DCA|=α i trójkąt ADC jest równoramienny, podobnie jak trójkąt CDB. Niech E będzie środkiem boku AC. Wówczas z twierdzenia Pitagorasa w trójkącie EDC mamy |ED|=15. Z drugiej strony z twierdzenia Pitagorasa w trójkątach ACF i CDF mamy |CF|2 = 252–DF2 = 402–(25+|DF|)2, skąd |DF|=7, |CF|=24. Ostatecznie PABC = PADC + PCDB = 300 + 168 = 468.
Zad. 2. Niech N będzie punktem na boku BC takim, że |∡MNC| = 30°. Mamy wówczas |∡AMN| = 60° i dalej |∡NMC| = 15°. Oznacza to równość długości odcinków AM, MB, MN, NC. Zauważmy teraz, że trójkąt AMN jest równoboczny, bo |∡AMN| = 60°, a stąd kąty ANB i ANC są proste. Ostatecznie w trójkącie prostokątnym i równoramiennym ANC mamy |∡ACN| = 45°, skąd szukany kąt ACM ma miarę 30°.
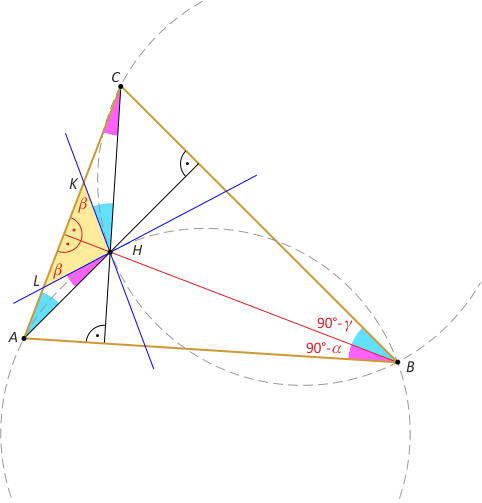
Zad. 3. Rozważmy trójkąt ostrokątny. Łatwo zauważyć że |∡ACH| = |∡HBA| = 90°–α = |∡LHA| (kąt dopisany do okręgu) oraz analogicznie |∡CAH| = |∡HBC| = 90°–γ = |∡KHC| (kąt dopisany do okręgu). Wynika stąd równość kątów zewnętrznych LKH i KLH. Przypadek trójkąta rozwartokątnego rozpatrujemy analogicznie, a trójkąt prostokątny nie spełnia warunków zadania.
Zad. 4. (wolna amerykanka) Zauważmy, że na czworokącie KDLC można opisać okrąg. Łatwo zauważyć podobieństwo trójkątów ABC, ADC, CDB i KDL. Skala podobieństwa trójkątów ABC i KDL wynosi k = |KD|:15. Z własności trójkata prostokątnego mamy: |AC|2 = |AD|·|AB| = |AD|·(|AD|+16) = 225, skąd |AD|=9. Z twierdzenia kosinusów w trójkącie ADK mamy: |KD|2 = 100+81–180·cosα = 181–180·(3/5) = 73. Łatwo zauważyć, że trójkąt ABC jest pitagorejski i |BC| = 20. Ostatecznie PKDL = k2·PABC = (73/225)·150 = 146/3 = 48 i 2/3.
Czy wiesz, kto z wrocławskich matematyków został uwiecz-niony na tym znakomitym portrecie w piżamie? Kto jest autorem tego obrazu? Gdzie można go obejrzeć?
Jako młody chłopak Knaster ożenił się z poznaną w Paryżu Marią Morską - muzą Skaman-drytów (zm. w 1945 roku). W czasach wrocła-wskich jego drugą żoną była Regina Lewandowska. Pierwszej żonie Knastera poświęcona jest książka Hanny Faryny-Paszkiewicz "Opium życia".
Steinhaus twierdził, że nazwisko Knaster brzmi w dopeł-niaczu Knastra, a sam Knaster upierał się przy formie Knastera. 
