Zaad. 1. Państwo Kowalscy, podróżując samolotem linii Biełka, mieli razem 94 kg bagażu. Pan Kowalski zapłacił 15 zł za nadbagaż, a pani Kowalska - 20 zł. Gdyby pan Kowalski podróżował sam z bagażem obojga, to zapłaciłby za nadbagaż 135 zł. Ile kilogramów bagażu może bezpłatnie wziąć ze sobą pasażer na pokład samolotu linii Biełka?
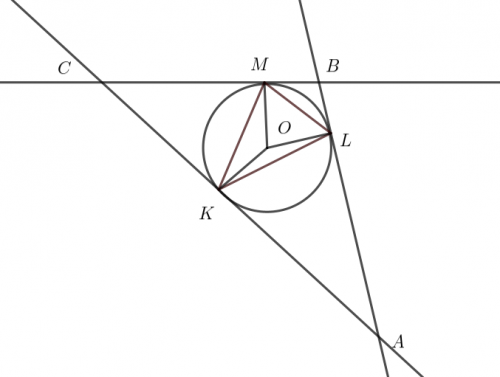
Zad. 2. Okrąg został podzielony w stosunku 5:9:10. W punktach podziału poprowadzono styczne. Oblicz miary kątów trójkąta, którego wierzchołkami są punkty przecięcia tych stycznych.
Zad. 3. Wykaż, że liczba 13 + 23 + 33 + ··· + 20233 + 20243 jest podzielna przez 2025.
W czerwcu punkty zdobyli:
- 3 – Emilia Cichowska II LO Lubin, Zuzanna Czapiewska ZSB Słupsk, Jagoda Janiś LO Góra, Joanna Nowakowska LO Aslan Głogów, Liliana Ottlik III LO Wrocław, Paweł Prasal III LO Leszno, Gabriela Pułecka V LO Wrocław, Cezary Rębiś ZSE Radom, Miłosz Zakrzewski LO Tuchola;
- 2 – Artur Bumażnik ZSE Jelenia Góra, Mikołaj Idzikowski I LO Ostrzeszów, Oliwier Roszkowski X LO Wrocław.
Pozostali uczestnicy otrzymali poniżej 1 punktu.
Zad. 1. Niech x oznacza liczbę sztuk bagażu, jaką każdy pasażer może wziąć bezpłatnie do samolotu. Państwo Kowalscy zabrali do samolotu łącznie 94 kilogramy bagażu, w tym 94–2x kg bagażu za 35 zł. Wynika stąd, że kilogram płatnego bagażu kosztuje 35:(94–2x). Gdyby do samolotu wsiadł sam pan Kowalski, zapłaciłby za 94–2x kilogramów bagażu 135 zł, więc za 1 kg opłata wynosiłaby 135:(94–2x). Przyrównując te opłaty, otrzymujemy równanie 35:(94–2x) = 135:(94–2x), skąd x=40 kg. Każdy pasażer może wziąć bezpłatnie ze sobą bagaż ważący 40 kg.
Zad. 2. Niech O będzie środkiem, a K, M, N będą punktami podziału okręgu. Niech A, B, C będą wierzchołkami trójkąta otrzymanego ze stycznych. Proporcja podziału okręgu jest taka sama jak proporcja podziału kata pełnego kątami środkowymi o ramionach przechodzących przez punkty styczności, czyli |∡KOL|:|∡LOM|:|∡MOK| = 9:5:10. Stąd |∡KOL|=135°, |∡LOM|=75° i |∡MOK|=150°. W czworokącie KOLA mamy |∡OKA| = |∡OLA|=90°, zatem |∡KAL| = 360°–2·90°–|∡KOL| = 180°–135° = 45°. Podobnie obliczamy miary pozostałych kątów: |∡LBM|=105° i |∡MCK|=30°. Ostatecznie miary kątów trójkąta wynoszą 30°, 45° i 105°.
Zad. 3. Zauważmy, ze 13 + 23 + ⋯ + n3 = (1+2+⋯+n)2 = (1/2n(n+1))2. Zatem 13 + 23 + 33 +···+ 20233 + 20243 = (2024·2025:2)2 = (1012·2025)2. Liczba 1012·2025 jest podzielna przez 2025, zatem wynik zadania również.







