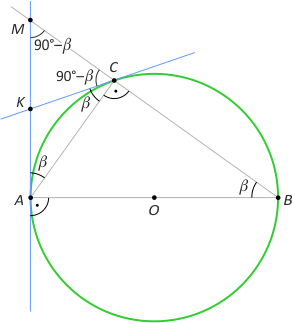
Zad. 1. W trójkącie ABC kąt A ma miarę 40°. Dwusieczna kąta A i dwusieczna kąta zewnętrznego przy wierzchołku C przecinają się w punkcie M. Oblicz miarę kąta BMC.
Zad. 2. Dany jest okrąg o średnicy AB i jego dowolny punkt C (różny od A i B). Styczna do okręgu w punkcie A przecina prostą BC w punkcie M. Wykaż, że styczna do okręgu w punkcie C dzieli odcinek AM na połowy.
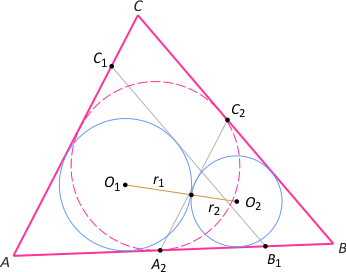
Zad. 3. Dwa okręgi styczne zewnętrznie leżą wewnątrz trójkąta i każdy z nich jest styczny do jego dwóch boków (nie tych samych). Wykaż, że suma promieni tych okręgów jest większa od promienia okręgu wpisanego w trójkąt.
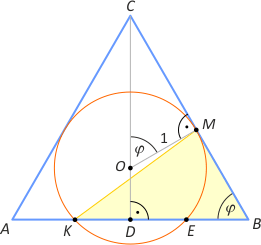
Zad. 4. (wolna amerykanka) W trójkącie równoramiennym (|AC|=|BC|) tangens kąta przy podstawie wynosi 8/15. Okrąg o promieniu 1 wpisany w kąt C jest styczny do boku BC w punkcie M i odcina od podstawy odcinek KE (K leży między A i E). Oblicz pole trójkąta KMB wiedząc, że |MB|=15/8.
Za zadania 1-3 punkty otrzymali:
- 30 - Dominik Bysiewicz (student UJ) i Jacek Bagiński (nauczyciel matematyki, I LO Kraków) ,
- 28 - Tadeusz Porzucek (emerytowany nauczyciel, Gostyń),
- 20 - Elżbieta Grzechnik (emerytowany nauczyciel, Radom), Mikołaj Popek (student UAM) i Janusz Wieczorek (emerytowany nauczyciel, Sandomierz),
- 10 - Joanna Koścień (nauczyciel SP 14, Piekary Śląskie), Filip Derejski (I LO Kraków) i Adam Wrzesiński (terapeuta, Bielsko-Biała).
Za zadanie 4 po 10 pkt. otrzymali: Jacek Bagiński, Dominik Bysiewicz, Mikołaj Popek, Tadeusz Porzucek oraz Janusz Wieczorek.
Gratulacje!
Zad. 1. Zauważmy, że punkt M jest środkiem okręgu dopisanego do trójkąta, a półprosta CM jest dwusieczną kąta zewnętrznego przy wierzchołku C. Mamy zatem |∡CBM| = (180°– β)/2 = 90°– β/2 oraz |∡MCB| = (180°–γ)/2 = 90° –γ/2. Z twierdzenia o sumie kątów wewnętrznych dla czworokąta ABMC otrzymujemy |∡BMC| = 360°–40°–β–(90°–β/2)–γ–(90°–γ/2) = 140°–(β+γ)/2 = 140°–(180°–40°)/2 = 70°.
Zad. 2. Niech prosta KC będzie styczną do okręgu. Wówczas kąty dopisane KCA i KAC są przystające i mają miarę β. Oznacza to, że trójkąt KAC jest równoramienny i |KC| = |KA|. Dalej zauważmy, że |∡KMC| = |∡AMB| = 90°–β oraz |<KCM| = 90°–β. Oznacza to, że trójkąt KCM jest też równoramienny i |KC| = |KM|, a stąd (i z przechodniości równości) |KA| = |KM|, c. b. d. o.
Zad. 3. Poprowadźmy do obu okręgów styczne B1C1 oraz A2C2 równoległe do odpowiednich boków trójkąta. Zauważmy, że trójkąty AB1C1 oraz A2BC2 są podobne do trójkąta ABC w skalach odpowiednio k1 = r1/r oraz k2 = r2/r. Trójkąty AB1C1 oraz A2BC2 mają wspólną część, bo inaczej okręgi nie miałyby punktu wspólnego, zatem |AB1|+|A2B| > |AB|. Dzieląc obie strony nierówności przez |AB|, otrzymujemy |AB1|/|AB| + |A2B|/|AB| > 1, co jest równoważne k1+k2 > 1. Ostatecznie otrzymujemy r1/r + r2/r > 1, skąd wynika teza r1 + r2 > r.
Zad. 4. (wolna amerykanka) Zauważmy, że trójkąty COM i CDB są podobne, przy czym |∡COM| = |∡DBC| = φ. Zatem w trójkącie OMC mamy |MC|/|OM| = tgφ, skąd |MC| = 8/15. Dalej |BC| = |BM|+|MC| = 289/120. Z układu równań sinφ/cosφ = 8/15 oraz (sinφ)2+(cosφ)2 = 1 otrzymujemy sinφ = 8/17 oraz cosφ = 15/17. Z trygonometrii w trójkącie CDB mamy |DB| = |BC|·cosφ = 17/8, skąd |AB| = 17/4. Uwzględniając, że |AK| = |EB|, z tw. o stycznej i siecznej okręgu mamy |BM|2 = |KB|·|EB| = (|AB|–|AK|)·|EB| = (|AB|–|EB|)·|EB|, a po podstawieniu 225/64 = (17/4–|EB|)·|EB|. Rozwiązując ostatnie równanie, otrzymujemy |EB| = 9/8 (wiemy, że |EB| < |DB| = 17/8). Ostatecznie szukane pole wynosi PKBM = |KB|·|BM|·sinφ/2 = 375/272.
Czy wiesz, kto z wrocławskich matematyków został uwiecz-niony na tym znakomitym portrecie w piżamie? Kto jest autorem tego obrazu? Gdzie można go obejrzeć?
Jako młody chłopak Knaster ożenił się z poznaną w Paryżu Marią Morską - muzą Skaman-drytów (zm. w 1945 roku). W czasach wrocła-wskich jego drugą żoną była Regina Lewandowska. Pierwszej żonie Knastera poświęcona jest książka Hanny Faryny-Paszkiewicz "Opium życia".
Steinhaus twierdził, że nazwisko Knaster brzmi w dopeł-niaczu Knastra, a sam Knaster upierał się przy formie Knastera. 
