Zapraszamy do udziału w jubileuszowych XX Mistrzostwach Polski w Geometrii Elementarnej, które będą rozegrane we Wrocławiu 4 VI. Zgłoszenia są przyjmowane do 25 V. Tu jest formularz zgłoszeniowy dla zawodników i ich nauczycieli.
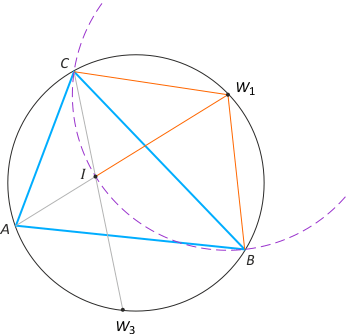
Zad. 1. Na trójkącie ABC opisano okrąg. Wierzchołki podzieliły okrąg na trzy łuki. Rozważmy okręgi, których środkami są środki tych łuków i które przechodzą przez dwa wierzchołki trójkąta. Wykaż, że okręgi te mają punkt wspólny.
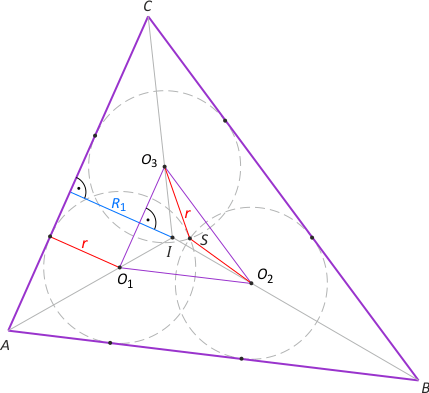
Zad. 2. Trzy okręgi o promieniu r mają punkt wspólny i każdy z nich jest styczny do dwóch boków trójkąta ABC. Promień okręgu opisanego na trójkącie wynosi R. Oblicz długość promienia okręgu wpisanego w trójkąt.
Zad. 3. Niech K, L i M będą odpowiednio środkami wysokości AH1, BH2 i CH3 w trójkącie ostrokątnym ABC. Znajdź sumę miar kątów LH1M, MH2K i KH3L.
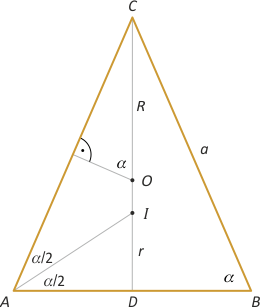
Zad. 4. (wolna amerykanka) Znajdź kąt przy podstawie trójkąta równoramiennego ABC, wiedząc że stosunek promienia okręgu wpisanego w ten trójkąt do promienia okręgu opisanego na tym trójkącie wynosi 3/8.
Za zadania 1-3 punkty otrzymali:
- 30 - Dominik Bysiewicz (student UJ), Tadeusz Porzucek (emerytowany nauczyciel, Gostyń), Elżbieta Grzechnik (emerytowany nauczyciel, Radom) i Mikołaj Popek (student UAM),
- 18 - Jacek Bagiński (nauczyciel matematyki, I LO Kraków).
Za zadanie 4 punkty otrzymali:
- 10 - Dominik Bysiewicz, Elżbieta Grzechnik, Janusz Wieczorek (emerytowany nauczyciel, Sandomierz) oraz Mikołaj Popek,
- 8 - Jacek Bagiński i Tadeusz Porzucek.
Gratulujemy!
Zad. 1. Zauważmy, że środki łuków są punktami przecięcia okręgu z dwusiecznymi kątów trójkąta. Szukanym punktem wspólnym okręgów jest środek I okręgu wpisanego w trójkąt ABC, bowiem z zasady trójliścia (patrz luty 2014, zad. 3) mamy |W1I| = |W1C| = |W1B|. Analogicznie |W2I| = |W2C| = |W2A| oraz |W3I| = |W3A| = |W3B|.
Zad. 2. Niech S będzie punktem wspólnym okręgów o środkach O1, O2 i O3. Wówczas promień tych okręgów r = |SO1| = |SO2| = |SO3| jest jednocześnie promieniem okręgu opisanego na trójkącie O1O2O3. Łatwo zauważyć, że środki okręgów wpisanych w trójkąty ABC i O1O2O3 pokrywają się, a ponadto boki tych trójkątów są w odpowiednich parach równoległe i oddalone o r. Oznacza to podobieństwo tych trójkątów, a z niego otrzymujemy proporcję R1:R = (R1–r):r. Ostatecznie R1 = Rr/(R–r).
Zad. 3. Zauważmy, że odcinki MM1 i M1L są liniami średnimi trójkątów odpowiednio CH3B i CH2B równoległymi do podstaw odpowiednio AB i AC, skąd |∡MM1H1| = β i |∡LM1B| = γ. Dodatkowo |∡HLM1| = |∡HMM1| = 90° = |∡HH1M1|. Oznacza to, że punkty H, L, M1, H1 i M leą na jednym okręgu o średnicy HM1 (dlaczego?). To z kolei oznacza, że kąt LH1M wpisany w ten okrąg jest oparty na łuku ML i ma miarę taką samą jak kąt MM1L, czyli α. Analogicznie otrzymujemy |∡KH3L| = γ oraz |∡MH2K| = β. Ostatecznie szukana suma kątów wynosi 180°.
Zad. 4. Skorzystamy ze wzoru Eulera (luty 2014, zad. 3): |OI|2 = R2–2Rr. Z twierdzenia sinusów mamy sinα = a/2R, a z proporcji trygonometrycznych w trójkącie CDB mamy sinα = |CD|/a = (R+r+|OI|)/a = (R+r+√(R2–2Rr))/a. Otrzymujemy zatem równanie a/2R = (R+r+√(R2–2Rr))/a, skąd po podstawieniu r = 3R/8 otrzymujemy a2 = 15R2/4. Jeszcze raz stosując twierdzenie sinusów, mamy 4R2(sinα)2 = 15R2/4, skąd sinα = √15/4. W przypadku trójkąta rozwartokątnego mamy równanie a/2R = (R+r–√(R2–2Rr))/a, skąd sinα = √7/4.
Czy wiesz, kto z wrocławskich matematyków został uwiecz-niony na tym znakomitym portrecie w piżamie? Kto jest autorem tego obrazu? Gdzie można go obejrzeć?
Jako młody chłopak Knaster ożenił się z poznaną w Paryżu Marią Morską - muzą Skaman-drytów (zm. w 1945 roku). W czasach wrocła-wskich jego drugą żoną była Regina Lewandowska. Pierwszej żonie Knastera poświęcona jest książka Hanny Faryny-Paszkiewicz "Opium życia".
Steinhaus twierdził, że nazwisko Knaster brzmi w dopeł-niaczu Knastra, a sam Knaster upierał się przy formie Knastera. 
