Zad. 1. Niech M oznacza środek boku BC w trójkącie równobocznym ABC. Na odcinkach CM i AB obrano punkty odpowiednio P i R takie, że |AR| = |CP|. Oblicz sumę miar kątów AMR, CRM i PAM.
Zad. 2. Niech CH oznacza wysokość w trójkącie ABC. Wiedząc, że |AH|=1, |HB|=4 oraz że kąt B jest dwa razy większy od kąta ACH, oblicz długość AC.
Zad. 3. Na boku AB trójkąta równobocznego ABC obrano punkt D (różny od śrdodka boku), a następnie na odcinkach AD i DB jako na średnicach zbudowano okręgi, które przecięły boki AC i BC odpowiednio w punktach K i N. Prosta KN przecina wtórnie te okręgi w punktach L i M (przy czym L leży między K i M). Wykaż, że |LM|2 = |KL|·|MN|.
Zad. 4. (wolna amerykanka) Dany jest okrąg o promieniu R i dwie jego cięciwy AB i AC. Na prostej AB obrano punkt M, którego odległość od prostej AC równa jest |AC|, a na prostej AC obrano punkt N, którego odległość od prostej AB jest równa |AB|. Oblicz długość MN.
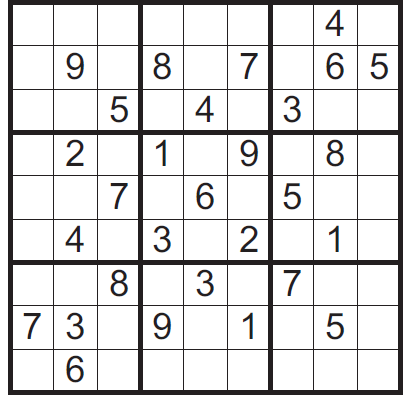
To zabawny samouczek, który zaczynając się niewinnie intrygującą historyjką, krok po kroku, poczynając od najłatwiejszych łamigłówek, prowadzi nas w szpony, nie bójmy się użyć tego słowa, uzależnienia.
