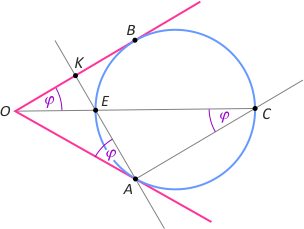
Zad. 1. Dany jest kąt o wierzchołku O i okrąg styczny do jego ramion w punktach A i B. Półprosta o początku w A równoległa do OB przecina okrąg w punkcie C. Odcinek OC przecina okrąg w punkcie E. Proste AE i OB przecinają się w K. Wykaż, że |OK| = |KB|.
Zad. 2. W prostokącie ABCD punkt M jest środkiem boku AD, a punkt K dzieli bok AB w stosunku 2:1. Odcinki DK i CM przecinają się w punkcie O. Wiedząc, że PMOD = 6, oblicz pole czworokąta KBCO.
Zad. 3. W trójkącie ABC mamy: |AB|+|BC|=11, |∡B|=60°, a promień okręgu wpisanego w ABC wynosi 2/√3. Niech |AB|>|BC|. Oblicz długość wysokości opuszczonej z wierzchołka A.
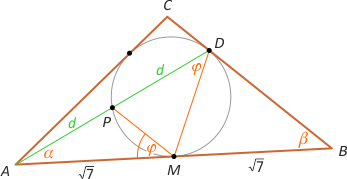
Zad. 4. (wolna amerykanka) W trójkąt ABC wpisano okrąg. Punkt styczności dzieli bok AB na odcinki o długości √7. Z kolei okrąg dzieli odcinek łączący wierzchołek A z punktem styczności do boku BC na połowy. Oblicz promień okręgu.
W tym miesiącu za zadania 1-3 punkty otrzymali:
- 30 - Dominik Bysiewicz (student matematyki na UJ), Robert Ciężabka (korepetytor, Osiek Jasielski), Radosław Górzyński (uczeń I LO Lubin), Elżbieta Grzechnik (emerytowana nauczycielka z Radomia), Mikołaj Popek (student UAM), Tadeusz Porzucek (emerytowany nauczyciel z Gostynia),
- 20 - Marzena Wąsiewicz (nauczycielka z Kajetan),
- 10 - Filip Derejski (student mechatroniki na AGH w Krakowie).
Za zadanie 4 po 10 pkt. otrzymali: Dominik Bysiewicz, Robert Ciężabka, Radosław Górzyński, Elżbieta Grzechnik, Zygmunt Krawczyk (emerytowany nauczyciel ze Szprotawy), Tadeusz Porzucek, Mikołaj Popek oraz Marzena Wąsiewicz. Gratulacje!
Zad. 1. Zauważmy równość kątów o wierzchołkach w punktach A, C i O. Pierwsze dwa mają równe miary, bo kąt C jest wpisany w okrąg, a A jest dopisany do okręgu i są oparte na tym samym łuku. Równość miar drugiej pary kątów wynika z równoległości prostych OB i AC. Z twierdzenia o stycznej i siecznej (tzw. potęga punktu względem okręgu) mamy |KB|2 = |KE|·|KA|, zaś z podobieństwa trójkątów OKE i OKA (kkk) mamy |OK|:|OE| = |KA|:|OA|. Ale |OA|=|OB|, stąd |OK|:|OE| = |KA|:|OB|, skąd |OK|2 = |KA|·|KE|, zatem |KB|2 = |OK|2, a stąd wynika teza.
Zad. 2. Wprowadźmy oznaczenia jak na rysunku poniżej. Przedłużmy odcinki DK i BC do punktu L. Niech MN będzie linią środkową trójkąta AKD. Wówczas |MN| = a i |MD| = b. Kąty MDN i BLK są przystające, stąd trójkąty MND i KLB są przystające (cecha kkk), a zatem |BL| = b. Otrzymaliśmy trójkąty podobne MOD i OLC w skali k = 1/3. Rozważmy trapez MNCD. Zachodzi PMOD·PONC = PMNO·POCD, ale PMOD = PONC, zatem PONC = √(PMNO· POCD). Trójkąty MNO i OCD są podobne w skali 1/3, skąd otrzymujemy 6 = √(PMNO · PMNO), a stąd PMNO = 2. Ostatecznie POKBC = PCOL – PKBL = 9·6–(6+2) = 46.
Zad. 3. Wprowadźmy oznaczenia jak na rysunku poniżej. Z własności okręgu wpisanego w trójkąt mamy |KB| = p–b, gdzie p oznacza połowę obwodu trójkąta. Z własności trójkąta ekierkowego mamy p–b = 2. Z drugiej strony 2p = a+b+c = b+11 = p–2+11, skąd p=9, a b=7. Ze wzoru Herona mamy PABC = √(9(9–a)(9–c)·2). Z drugiej strony PABC = rp = 18:√3. Uwzględniając, że a = 11–c, otrzymujemy równanie √(9(c–2)(9–c)·2) = 18:√3, skąd c=8 oraz a=3. Ostatecznie ha = 2PABC/a = 4√3.
Zad. 4. (wolna amerykanka) Z twierdzenia o stycznej i siecznej (tzw. potęga punktu względem okręgu) mamy |AM|2 = |AP|·|AD|, czyli 7=2d2, skąd d = √(7/2). Zauważmy teraz, że MP jest linią środkową trójkąta ABD oraz |MP| = |BD|/2 = |MB|/2 = √7/2. Z przystawania kątów AMP (dopisanego do okręgu) i ADM (wpisanego w okrąg) wynika podobieństwo trójkątów AMP i AMD (kkk). Otrzymujemy zatem proporcję |PM|:|AM| = |DM|:|AD|, skąd |DM| = |PM|·|AD|/|AM| = |AD|/2 (bo |AM|=|MB|=|BD|). Oznacza to, że trójkąt PMD jest równoramienny o bokach √(7/2), √(7/2) i √7/2. Szukany promień okregu wpisanego w trójkąt ABC znajdziemy jako promień okręgu opisanego na trójkącie PMD. Ze wzoru Herona PPMD = (7·√7)/16, a R = abc/4P =
√(7/2)·√(7/2)·√7/2] : [4·(7/16)·√7] = 1.
Czy wiesz, kto z wrocławskich matematyków został uwiecz-niony na tym znakomitym portrecie w piżamie? Kto jest autorem tego obrazu? Gdzie można go obejrzeć?
Jako młody chłopak Knaster ożenił się z poznaną w Paryżu Marią Morską - muzą Skaman-drytów (zm. w 1945 roku). W czasach wrocła-wskich jego drugą żoną była Regina Lewandowska. Pierwszej żonie Knastera poświęcona jest książka Hanny Faryny-Paszkiewicz "Opium życia".
Steinhaus twierdził, że nazwisko Knaster brzmi w dopeł-niaczu Knastra, a sam Knaster upierał się przy formie Knastera. 
