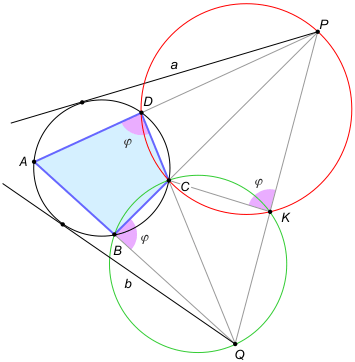
Zad. 1. Dany jest czworokąt wpisany w okrąg. Proste zawierające przeciwległe boki czworokąta przecinają się w punktach P i Q. Oblicz |PQ|, wiedząc, że odcinki styczne do okręgu poprowadzone z P i Q mają długości odpowiednio a i b.
Zad. 2. W czworokącie ABCD mamy: |AB| = a oraz |AD| = b. Boki BC, CD i AD są styczne do okręgu, którego środek znajduje się w połowie boku AB. Oblicz |BC|.
Zad. 3. W trójkąt ABC wpisano okrąg. M i N są punktami styczności tego okręgu odpowiednio z bokami BC i BA. Niech K będzie punktem przecięcia dwusiecznej kąta A z prostą MN. Wykaż, że kąt AKC jest prosty.
Zad. 4. (wolna amerykanka) Oblicz kąt ostry rombu, w którym długość boku jest średnią geometryczną długości przekątnych.
Za rozwiązania zadań 1-3 następujące liczby punktów zdobyli:
- 30 - Robert Ciężabka (student AGH) i Michel Migas (student matematyki na PW),
- 28 - Tadeusz Porzucek (emerytowany nauczyciel, Gostyń),
- 20 - Szymon Kaźmierowski (nauczyciel, IV LO Elbląg), Mikołaj Sikora (III LO Tarnów) i Paweł Wesołowski (II LO Końskie).
W kategorii "wolnej amerykanki" maksymalną liczbę punktów uzyskali: Robert Ciężabka, Szymon Kaźmierowski, Zygmunt Krawczyk (nauczyciel, SLO Żary), Michel Migas, Tadeusz Porzucek, Mikołaj Sikora, Sabina Khady Sy (studentka nanotechnologii na UJ) i Wojciech Tomiczek (inżynier, Lipowa).
Gratulacje!
Zad. 1. Rozważmy okrąg opisany na trójkącie PDC. Punkt wspólny okręgu i odcinka PQ oznaczmy przez K. Zauważmy, że miary kątów CKP i ADC są równe, bo oba te kąty w sumie z kątem CDP dają kąt półpełny. Z drugiej strony miary kątów CBQ i ADC też są równe, bo czworokąt ABCD jest wpisany w okrąg. Oznacza to, że punkty B, Q, K i C leżą na jednym okręgu. Stosując twierdzenie o potędze punktu względem okręgu, otrzymujemy |PK|·|PQ| = |PC|·|PB| = a2 oraz |QK|·|QP| = |QC|·|QD| = b2. Dodając te równości stronami, otrzymujemy |PK|·|PQ| + |QK|·|QP| = a2+b2 i dalej |PQ|·(|PK|+|QK|) = a2+b2, skąd ostatecznie |PQ|2 = a2+b2. Zatem |PQ| = √(a2+b2).
Zad. 2. Zauważmy, że trójkąty prostokątne AOK i OBL są przystające, bo AO ≡ OB oraz OK ≡ OL. Oznacza to, że kąty OAD i OBC mają jednakowe miary. Z sumy kątów w czworokącie ABCD mamy α+β+γ = 180°. Stąd wynika, że |∡AOD| = γ oraz |∡BOC| = β. Oznacza to, że trójkąty AOD i BOC są podobne (kkk). Otrzymujemy zatem |AO|/|AD| = |BC|/|OB|. Po podstawieniu danych i prostym przekształceniu otrzymujemy |BC| = a2/4b.
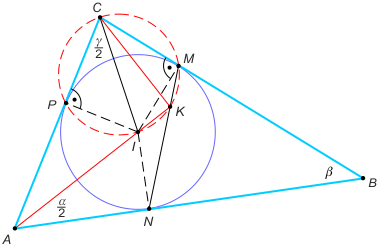
Zad. 3. Zauważmy, że trójkąt MNB jest równoramienny, skąd |∡MNB| = 90°– β/2. Z drugiej strony kąt ten jest zewnętrzny dla trójkąta AKN, zatem α/2 + |∡AKN| = 90°– β/2. Stąd |∡AKN| = γ/2. Oznacza to, że punkty I, K, M, C są współokręgowe. Współokręgowe są również punkty P, I, M, C, przy czym CI jest średnicą tego okręgu. Wszystkie punkty leżą zatem na jednym okręgu, a stąd wynika teza, bo kąt IKC jest oparty na średnicy IC.
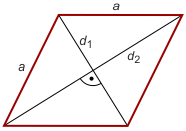
Zad. 4. Z założenia oraz z twierdzenia Pitagorasa otrzymujemy równanie a = √(d1·d2) = √(d21 + d22)/2, a po przekształceniach a = (d1/d2)2 – 4(d1/d2) + 1. Zauważmy, że d1/d2 = tg(α/2). Rozwiązując powyższe równanie kwadratowe i uwzględniając, że α/2 < 45°, otrzymujemy tg(α/2) = 2–√3. Stosując wzór na tangens podwojonego kąta tgα = (2tg(α/2))/(1-tg(α/2)) otrzymujemy tgα = 1/√3, zatem α = 30°.
Czy wiesz, kto z wrocławskich matematyków został uwiecz-niony na tym znakomitym portrecie w piżamie? Kto jest autorem tego obrazu? Gdzie można go obejrzeć?
Jako młody chłopak Knaster ożenił się z poznaną w Paryżu Marią Morską - muzą Skaman-drytów (zm. w 1945 roku). W czasach wrocła-wskich jego drugą żoną była Regina Lewandowska. Pierwszej żonie Knastera poświęcona jest książka Hanny Faryny-Paszkiewicz "Opium życia".
Steinhaus twierdził, że nazwisko Knaster brzmi w dopeł-niaczu Knastra, a sam Knaster upierał się przy formie Knastera. 
