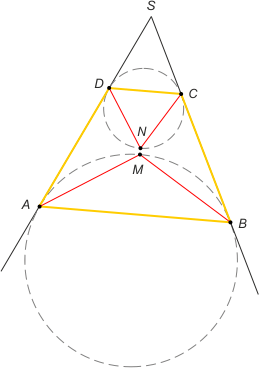
Zad. 1. Do dwóch okręgów o różnych promieniach poprowadzono wspólne styczne zewnętrzne. Wykaż, że w czworokąt o wierzchołkach w punktach styczności można wpisać okrąg wtedy i tylko wtedy, gdy okręgi są styczne zewnętrznie.
Zad. 2. Wysokość BH i środkowa BD tworzą równe kąty odpowiednio z bokami AB i BC. Znajdź promień okręgu opisanego na trójkącie ABC, wiedząc, że środkowa BD ma długość m.
Zad. 3. W trapezie ABCD punkt E jest środkiem podstawy AB, a punkt F - środkiem podstawy DC. Wykaż, że odcinek łączący punkty przecięcia przekątnych czworokątów AEFD i EBCF jest równoległy do podstaw trapezu.
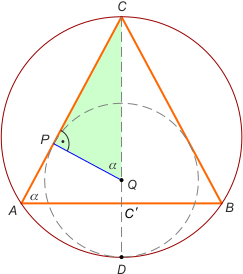
Zad. 4. (wolna amerykanka) W okrąg wpisano trójkąt równoramienny o podstawie długości a i kącie przy podstawie rozwartości α. Oblicz długość promienia okręgu stycznego jednocześnie do ramion trójkąta i okręgu na nim opisanego.
Za zadania 1-3 punkty uzyskali:
30 pkt. - Michel Migas (student PW) oraz Tadeusz Porzucek (emerytowany nauczyciel, Gostyń),
20 pkt.- Iwona Gruszecka (nauczycielka matematyki, CLV LO Warszawa).
Za zadanie 4 10 pkt. uzyskali: Michel Migas, Tadeusz Porzucek oraz Zygmunt Krawczyk (nauczyciel, SLO Żary).
Gratulacje!
Zad. 1. Niech S będzie punktem przecięcia stycznych, a M - środkiem łuku AB zawartego w trójkącie ASB. Z równości miar kątów MAB i ABM w trójkącie równoramiennym ABM wynika równość miar kątów dopisanych MAD i MBC. Oznacza to, że AM i BM są dwusiecznymi kątów BAD i ABC. Z drugiej strony niech N będzie środkiem łuku DC leżącego na zewnątrz trójkąta SDC. Analogicznie dowodzimy, że CN i DN są dwusiecznymi kątów BCD i CDA. Zatem gdy punkty M i N się pokrywają, to dwusieczne kątów czworokąta ABCD przecinają się w jednym punkcie. Stąd teza.
Zad. 2. Niech O będzie środkiem okręgu opisanego na trójkącie ABC, a E - punktem wspólnym okręgu i dwusiecznej kąta B. Zauważmy, że odcinek BH jest równoległy do OE (jako wysokość i symetralna boku AC). Z założenia wynika równość miar kątów HBE i EBD, zatem równe są miary kątów HBE i OBE (jako naprzemianległe). Oznacza to, że trójkąt BDE jest równoramienny. Z drugiej strony równoramienny jest trójkąt OEB i kąty EBO oraz EBM mają równe miary, skąd wynika, że O i M się pokrywają. AC jest zatem średnicą, a kąt B jest prosty. Zatem promień ma długość m.
Zad. 3. Z podobieństwa trójkątów DPF i APE (cecha kkk) otrzymujemy |FP|:|PA| = |DF|:|AE|. Analogicznie z podobieństwa trójkątów FQC i EQB mamy |FQ|:|QB| = |FC|:|EB|. Wobec określenia punktów E i F mamy |DF| = |FC| oraz |AE| = |EB|, skąd otrzymujemy w trójkącie ABF proporcję |FP|:|PA| = |FQ|:|QB|. Na mocy twierdzenia odwrotnego do twierdzenia Talesa mamy tezę.
Zad. 4. Niech Q jest środkiem okręgu stycznego do ramion trójkąta, a P - punktem styczności na jednym z ramion. Zauważmy, że kąt PQC ma miarę α (podobieństwo trójkątów prostokątnych ACC' i PCQ). Zatem r/CQ = cosα = r/2R–r, gdzie R jest promieniem okręgu opisanego na trójkącie ABC. Otrzymujemy r = 2Rcosα/1+cosα. Z twierdzenia sinusów mamy 2R = a/sin2α. Po podstawieniu i wykorzystaniu zależności na sinus podwojenego kąta otrzymujemy r = a/2sinα(1+cosα).
Czy wiesz, kto z wrocławskich matematyków został uwiecz-niony na tym znakomitym portrecie w piżamie? Kto jest autorem tego obrazu? Gdzie można go obejrzeć?
Jako młody chłopak Knaster ożenił się z poznaną w Paryżu Marią Morską - muzą Skaman-drytów (zm. w 1945 roku). W czasach wrocła-wskich jego drugą żoną była Regina Lewandowska. Pierwszej żonie Knastera poświęcona jest książka Hanny Faryny-Paszkiewicz "Opium życia".
Steinhaus twierdził, że nazwisko Knaster brzmi w dopeł-niaczu Knastra, a sam Knaster upierał się przy formie Knastera. 
