Zad. 1. Czy istnieje trójkąt o bokach długości 7 i 2, w którym wysokość opuszczona na trzeci bok jest średnią geometryczną pozostałych wysokości.
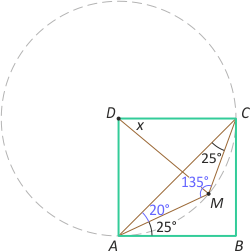
Zad. 2. Wewnątrz kwadratu ABCD obrano punkt M taki, że |∡ACM| = |∡MAB| = 25°. Znajdź miarę kąta MDC.
Zad. 3. Okrąg o środku D przechodzi przez wierzchołki A i B trójkąta ABC oraz przez środek O okręgu do tego trójkąta dopisanego i stycznego do boku BC. Wykaż, że punkty A, B, C i D leżą na jednym okręgu.
Zad. 4. (wolna amerykanka) Obwód czworokąta wypukłego ABCD wynosi 4. Wykaż, że jego pole jest nie większe niż 1.
W tym miesiącu za zadania 1-3 po 30 pkt. otrzymali: Dominik Bysiewicz (student matematyki na UJ), Robert Ciężabka (korepetytor, Osiek Jasielski), Radosław Górzyński (uczeń I LO Lubin), Elżbieta Grzechnik (emerytowana nauczycielka z Radomia), Mikołaj Popek (student UAM), Tadeusz Porzucek (emerytowany nauczyciel z Gostynia) oraz Marzena Wąsiewicz (nauczycielka z Kajetan).
Za zadanie 4 po 10 pkt. otrzymali: Dominik Bysiewicz, Robert Ciężabka, Radosław Górzyński, Elżbieta Grzechnik, Zygmunt Krawczyk (emerytowany nauczyciel ze Szprotawy), Mikołaj Popek, Tadeusz Porzucek oraz Marzena Wąsiewicz. Gratulacje!
Zad. 1. Oznaczmy pole trójkąta ABC przez S. Wówczas h1 = 2S/2 oraz h2 = 2S/7. Niech h będzie średnią geometryczną h1 i h2. Mamy h = √(h1·h2) = S·√(2/7). Z drugiej strony S = h·c/2, skąd otrzymujemy c = √14. Zauważmy, że nie zachodzi nierówność |AB| + |AC| > |BC|, bo 2+√14 < 7. Sprzeczność dowodzi, że taki trójkąt nie istnieje.
Zad. 2. Zauważmy, że |∡MAC|=20° i |∡AMC|=135°. Z drugiej strony kąt rozwarty ADC ma miarę 270°. Oznacza to, że kąt AMN jest wpisany w okrąg o środku w punkcie D i dalej |∡MDC|=40°, bo jest środkowy oparty na łuku CM.
Zad. 3. Wystarczy wykazać, że kąty ACB i ADB są przystające. Miara kąta wpisanego AOB jest równa |∡OBX| – |∡BAO| = |∡CBX|/2–|∡BAO| = (180°–β)/2 – α/2 = 90°–β/2–α/2 = γ/2. Oznacza to, że kąt środkowy ADB ma miarę γ, cbdo.
Zad. 4. Zauważmy, że GE jest linią średnią w trójkącie ABD i SAEH = SABD/4. Analogicznie SGFC = SBCD/4, a stąd SAEH + SGFC = SABCD/4. Z drugiej strony SEBF + SHGD = SABCD/4 i otrzymujemy SABCD = 2·SEFGH = |HF|·|EG|·sinφ ≤ |HF|·|EG| (*). Zauważmy teraz, że EG = EB+BC+CG oraz EG = EA+AD+DG (zapis boldem oznacza wektory). Po dodaniu tych równości mamy 2EG = BC+AD, skąd EG = (BC+AD)/2 i |EG| ≤ (|BC|+|AD|)/2. Analogicznie |HF| ≤ (|DC|+|AB|)/2. Podstawiając do (*), otrzymujemy SABCD ≤ |HF|·|EG| ≤ ((|BC|+|AD|)·(|DC|+|AB|))/4 ≤
((|BC|+|AD|+|DC|+|AB|)2 /4)/4 = 1. Ostatnie przejście polega na skorzystaniu z nierówności Cauchy'ego między średnimi geometryczną i arytmetyczną.
Czy wiesz, kto z wrocławskich matematyków został uwiecz-niony na tym znakomitym portrecie w piżamie? Kto jest autorem tego obrazu? Gdzie można go obejrzeć?
Jako młody chłopak Knaster ożenił się z poznaną w Paryżu Marią Morską - muzą Skaman-drytów (zm. w 1945 roku). W czasach wrocła-wskich jego drugą żoną była Regina Lewandowska. Pierwszej żonie Knastera poświęcona jest książka Hanny Faryny-Paszkiewicz "Opium życia".
Steinhaus twierdził, że nazwisko Knaster brzmi w dopeł-niaczu Knastra, a sam Knaster upierał się przy formie Knastera. 
