Zadanie 1. W trójkącie ostrokątnym ABC punkty E, F, G są środkami boków odpowiednio AC, BC i AB, a punkt H jest spodkiem wysokości opuszczonej z wierzchołka A. Wykaż, że czworokąt EGFH jest trapezem równoramiennym.
Zadanie 2. W trapezie ABCD (gdzie AB i CD to podstawy) ramię BC ma długość 8 cm. Odległość środka ramienia AD od prostej BC wynosi 10 cm. Oblicz pole tego trapezu.
Zadanie 3. W trapezie prostokątnym odległości środka okręgu weń wpisanego od końców ramienia nieprostopadłego do podstaw wynoszą 2 cm i 4 cm. Oblicz pole tego trapezu.
W październiku maksymalną liczbę punktów (czyli 30) uzyskali:
Jacek Bagiński (nauczyciel I LO Kraków), Włodzimierz Bąk (nauczyciel I LO Opole), Daria Bumażnik (uczennica II LO Jelenia Góra), Maciej Cebula (uczeń I LO Olesno), Anna Gudełajtis (uczennica II LO Opole), Katarzyna Kozińska (nauczycielka SP Leonardo da Vinci Wrocław), Krzysztof Sobków (nauczyciel II LO Opole) i Arkadiusz Wróbel (student Brwinów). Gratulujemy!
Pozostałe rozwiązania zawierały drobne usterki.
Zapraszamy do rozwiązywania zadań listopadowych.
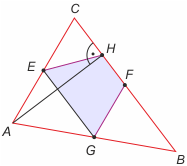Zadanie 1
Skorzystamy z dwóch znanych ze szkolnej geometrii faktów.
Fakt 1. Odcinek łączący środki dwóch boków trójkąta jest równoległy do trzeciego boku i dwa razy od niego krótszy.
Fakt 2. Środkowa przeciwprostokątnej jest od niej dwa razy krótsza.
Z F1 w trójkącie ABC mamy: EG || HF oraz FG = 1/2AC. Z F2 w trójkącie AHC mamy EH = 1/2AC. Stąd wynika teza.
Zadanie 2
Przez środek E boku AD prowadzimy prostą równoległą do BC, przecinającą proste AB i DC odpowiednio w punktach F i G. Zauważmy, że trójkąty AFE i GED są przystające z cechy kbk, bo ∡GDE ≡ ∡EAF (jako kąty naprzemianległe), ∡GED ≡ ∡AEF (jako kąty wierzchołkowe) i ED ≡ EA. Stąd PABCD = PFBCG = 10·8 = 80 cm2.
Zadanie 3
Zauważmy, że ∡COB = 90°, bo OB i OC leżą na dwusiecznych kątów, których suma wynosi 180°. Z twierdzenia Pitagorasa w ΔCOB mamy BC = 2√5, a z pola ΔCOB mamy r = 4√5/5. W trapez wpisano okrąg, więc AB+CD = AD+BC, a ponieważ AD = 2r, mamy PABCD = 1/2(AD+BC)·AD = 1/2(2r+BC)·2r = 72/5.
Czy wiesz, kto z wrocławskich matematyków został uwiecz-niony na tym znakomitym portrecie w piżamie? Kto jest autorem tego obrazu? Gdzie można go obejrzeć?
Jako młody chłopak Knaster ożenił się z poznaną w Paryżu Marią Morską - muzą Skaman-drytów (zm. w 1945 roku). W czasach wrocła-wskich jego drugą żoną była Regina Lewandowska. Pierwszej żonie Knastera poświęcona jest książka Hanny Faryny-Paszkiewicz "Opium życia".
Steinhaus twierdził, że nazwisko Knaster brzmi w dopeł-niaczu Knastra, a sam Knaster upierał się przy formie Knastera. 
