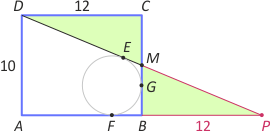
Zad. 1. Dany jest prostokąt ABCD o bokach długości |AB|=12 i |BC|=10. Niech M będzie środkiem boku BC. W prostokąt wpisano okrąg styczny do boków AB, BC i do odcinka MD. Oblicz jego promień.
Zad. 2. Dany jest kwadrat ABCD o boku długości 4. Niech K i M będą odpowiednio środkami boków AB i BC. Odcinki KC i MD przecinają się w punkcie P. Oblicz długość AP.
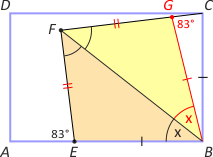
Zad. 3. Dany jest prostokąt ABCD. Na boku AB obrano punkt E taki, że |EB|=|BC|, a wewnątrz prostokąta punkt F taki, że |∡AEF|=83° oraz FB jest dwusieczną kąta EFC. Znajdź miarę kąta EBF.
Zad. 4. (wolna amerykanka) W kwadracie ABCD na bokach BC i CD obrano odpowiednio punkty E i F takie, że |∡FAE|=45° i |∡AFD|=70°. Oblicz miarę kąta AEF.
Zad. 1. Zauważmy, że trójkąty BPM i DMC są przystające (z cechy kbk) i |PM|=|MD|=13. Niech
|GB|=|BF| = r. Wówczas mamy |PE|=|PF|, skąd otrzymujemy równanie 13+(5–r) = 12+r. Ostatecznie r=3.
Zad. 2. Łatwo zauważyć, że odcinki DM i CK są prostopadłe, a trójkąty ANK i KBC - przystające. Odcinek AP jest środkową przeciwprostokątnej w trójkącie DNP, zatem A jest środkiem okręgu opisanego na tym trójkącie, a odcinek AP jest dwa razy krótszy niż DN, czyli ma długość 4.
Zad. 3. Obierzmy na odcinku FC punkt G tak, że |FE|=|FG|. Otrzymamy przystające trójkąty EBF i FBG (cecha bkb), skąd |∡BGC|=|∡AEF|=83° (kąty zewnętrzne). Otrzymaliśmy trójkąt równoramienny GBC, w którym |∡GBC|=14°. Ostatecznie kąt X ma miarę (90°–14°)/2 = 38°.
Zad. 4. Gdy obrócimy kwadrat ABCD wokół wierzchołka A o 90°, łatwo zauważymy przystawanie trójkątów AEF i AFE' (cecha bkb), skąd miara kąta X wynosi 65°.
Czy wiesz, kto z wrocławskich matematyków został uwiecz-niony na tym znakomitym portrecie w piżamie? Kto jest autorem tego obrazu? Gdzie można go obejrzeć?
Jako młody chłopak Knaster ożenił się z poznaną w Paryżu Marią Morską - muzą Skaman-drytów (zm. w 1945 roku). W czasach wrocła-wskich jego drugą żoną była Regina Lewandowska. Pierwszej żonie Knastera poświęcona jest książka Hanny Faryny-Paszkiewicz "Opium życia".
Steinhaus twierdził, że nazwisko Knaster brzmi w dopeł-niaczu Knastra, a sam Knaster upierał się przy formie Knastera. 
