Zadanie 1. Okrąg przechodzący przez wierzchołki A, B, C równoległoboku ABCD przecina proste AD i CD w punktach M i N. Punkt M jest odległy od punktów B, C i D odpowiednio o 4, 3 i 2. Oblicz długość MN.
Zadanie 2. W trójkącie równoramiennym ABC kąt B wynosi 120°. Znajdź długość wspólnej cięciwy okręgu opisanego na trójkącie ABC i okręgu przechodzącego przez punkt I będący środkiem okręgu wpisanego w ten trójkąt oraz spodki dwusiecznych kątów A i C, jeśli AC=1.
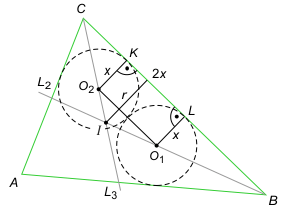
Zadanie 3. W trójkącie ABC dany jest bok BC o długości a oraz promień okręgu wpisanego r. Oblicz promień dwóch przystających okręgów wzajemnie stycznych, z których jeden jest styczny do boków BC i BA, a drugi - do boków BC i CA trójkąta.
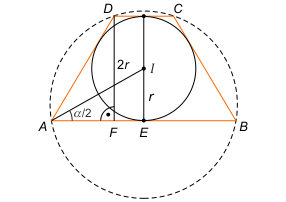
Zadanie 4. (wolna amerykanka) Dany jest trapez ABCD opisany na okręgu i jednocześnie wpisany w okrąg, w którym stosunek wysokości do promienia okręgu opisanego wynosi √(2/3). Oblicz rozwartości kątów tego trapezu.
Za zadania 1 - 3 maksymalną liczbę 30 pkt. uzyskali: Jacek Bagiński (nauczyciel, I LO Kraków), Włodzimierz Bąk (nauczyciel, I LO Opole), Michel Migas (student, Politechnika Warszawska), Krzysztof Sobków (nauczyciel, II LO Opole) i Iwona Gruszecka (nauczycielka, G 28 Wrocław). Zadanie 2 było trudne!
Za zadanie 4 maksymalną liczbę 10 pkt. zdobyli: Jacek Bagiński, Włodzimierz Bąk , Daria Bumażnik (uczennica, II LO Jelenia Góra), Michel Migas, Krzysztof Sobków, Tadeusz Porzucek (emeryt, Gostyń).
Gratulacje!
Zadanie 1. Zauważmy, że czworokąt NABC jest trapezem równoramiennym (bo jest wpisany w okrąg). Zatem kąty NMA i BMC są przystające (bo są wpisane w okrąg i oparte na przystających łukach AN i BC). Kąty MND i MBC też są przystające (jako wpisane oparte na łuku MC). Zatem trójkąty NDM i MBC są podobne (z cechy k-k-k) przy czym MN/MD = MB/MC, czyli po podstawieniu danych x/2= 4/3, skąd x = 8/3.
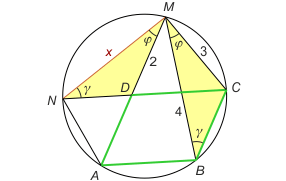
Zadanie 2. Rysunek podpowiada, aby MN obliczyć jako podwojoną wysokość w trójkącie OSM. Obliczmy zatem jego boki i pole.
Bok OM równy jest promieniowi R okręgu opisanego na trójkącie ABC, czyli wynosi R = √3/3 (jako bok trójkąta równobocznego AOB o wysokości 1/2). Natomiast MS = r = SL3. Rozważmy teraz trójkąt SL3L1 (rys. a). Ponieważ kąt AIC ma 150° (bo kąty A i C trójkąta ABC mają po 30°) oraz kąt L3IL1 też ma 150° (kąty wierzchołkowe), odpowiadający mu kąt środkowy ma 300°, a jego dopełnienie - kąt L3SL1 ma 60°. Zatem trójkąt L3L1S jest równoboczny (równoramienny SL3 = r = L3L1 z kątem 60°). Obliczymy teraz długość odcinka L3L1 (czyli także r=MS). Z podobieństwa trójkątów L3BL1 i ABC (rys. b) mamy tutaj BL1/L3L1 = BC/AC i podstawiając BC = √3/3, otrzymujemy L3L1 = BL1√3. Z kolei z twierdzenia o dwusiecznej BL1/L1C = AB/AC, czyli BL1/(√3/3 - BL1) = √3/3, skąd BL1 = (3-√3)/6. Zatem L3L1 = (3-√3)·√3/6 = (√3-1)/2.
Znamy już dwa boki trójkąta OSM: OM = √3/3 i MS = (√3-1)/2. Kolej na bok OS. Zauważmy, że OS = OB + BS = OB + SI - BI = R + r - BI. Z twierdzenia o dwusiecznej w trójkącie ADB mamy BI/ID = AB/AD, co przy BD = √3/6 daje BI/(√3/6-BI) = 2√3/3, skąd BI = (2√3-3)/3. Ostatecznie OS = (√3 + 3)/6.
Obliczając teraz pole trójkąta OSM na dwa sposoby (za pomocą wysokości opuszczonej na OS i ze wzoru Herona), otrzymujemy 1/2·(√3+3)/6 · (1/2·MN) = √(√3/2·√3/6·1/2·(2√3-3)/6), skąd MN = √(14√3 - 24).
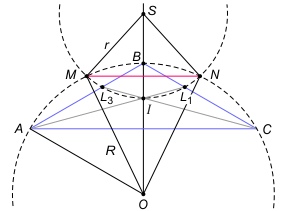
a)
b)
Zadanie 3. Rozważmy trójkąt CIB. Jego pole jest sumą pól trapezu CO2O1B i trójkąta O2IO1, Co zapisujemy równaniem 1/2ar = 1/2·x(a+2x) + 1/2·2x(r-x). Stąd x = ar/(a+2r).
Zadanie 4. Zauważmy, że trapez musi być równoramienny (bo jest wpisany w okrąg). Niech R oznacza promień okręgu opisanego na trapezie. Z założenia 2r/R = √2/3, a stąd R = r√6. Rozważmy trójkąt ABD. Zachodzi AB = 2AE. W trójkącie AEI mamy AE = r ctg(α/2), zatem AB = 2r ctg(α/2). Z twierdzenia sinusów mamy BD = 2r√6sinα, a w trójkącie AFD mamy AD = 2r/sinα. Dalej z twierdzenia kosinusów otrzymujemy równanie BD2 = AB2 + AD2 - 2 AB·AD·cosα, a po podstawieniu 24r2sin2α = 4r2·ctg2(α/2) + 4r2/sin2α - (8r2·ctg(α/2)·cosα)/sinα. Dzieląc obie strony przez 4r2 otrzymujemy 6sin2α = ctg2(α/2) + 1/sin2α - 2ctg(α/2)·ctgα. Korzystając ze wzoru ctgα = (ctg2(α/2) - 1)/2ctg(α/2), otrzymujemy równanie 6sin2α = 1/sin2α + 1. Uwzględniając, że α należy do przedziału (0, π/2), otrzymujemy rozwiązanie α = π/4.
Czy wiesz, kto z wrocławskich matematyków został uwiecz-niony na tym znakomitym portrecie w piżamie? Kto jest autorem tego obrazu? Gdzie można go obejrzeć?
Jako młody chłopak Knaster ożenił się z poznaną w Paryżu Marią Morską - muzą Skaman-drytów (zm. w 1945 roku). W czasach wrocła-wskich jego drugą żoną była Regina Lewandowska. Pierwszej żonie Knastera poświęcona jest książka Hanny Faryny-Paszkiewicz "Opium życia".
Steinhaus twierdził, że nazwisko Knaster brzmi w dopeł-niaczu Knastra, a sam Knaster upierał się przy formie Knastera. 
