Autor: Michał Śliwiński
nauczyciel w III LO we Wrocławiu
W tegorocznych zadaniach maturalnych znów pojawiły się, oględnie mówiąc, usterki! Nie świadczy to najlepiej o pracy Centralnej Komisji Egzaminacyjnej, daje zły przykład uczniom i stanowi dla nich dodatkowe, frustrujące utrudnienie... Szef CKE, matematyk - Marek Legutko podał się do dymisji. Zapowiedziano zmiany w systemie pracy komisji zadaniowych. Czy to rozwiąże sprawę?
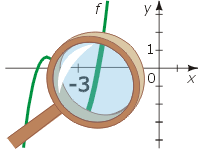W zadaniu 1 z poziomu rozszerzonego w treści zabrakło informacji o stopniu wielomianu. Bez tego zadania nie dało się rozwiązać! CKE, tłumacząc się dość kuriozalnie, pisze o dwóch możliwych poprawnych rozwiązaniach (!) - "standardowym" i "bardzo niestandardowym", a różnica między nimi polegać ma "tylko na interpretacji grubości kreski, którą narysowano wykres"!!! Czy ktoś coś z tego rozumie?
Niestety zdarzyli się całkiem nieźli z matematyki uczniowie, którzy pełnych danych umożliwiających jednoznaczne rozwiązanie zadania (a mieli słuszne prawo przecież tego właśnie oczekiwać) poszukiwali w treści zadania i rysunku, odczytywanym tak, jak uczono ich w szkole i jak każe uświęcona tradycją, wszechobowiązująca matematyczna umowa, a nie domyślając się dodatkowych ułatwień czy też analizując metodologicznie grubość kreski! Wielu z nich straciło w ten sposób sporo czasu i nerwów, a spora część w wyniku swoich wątpliwości po prostu zaniechała rozwiązywania tego zadania.
Jeśli chcemy zaznaczyć, że jakiś punkt nalezy do wykresu, standardowo stawiamy w tym miejscu na wykresie pełną kropkę. To rozstrzyga sprawę miejsc zerowych, ale w żaden sposób nie wpływa na rozstrzygnięcie kwestii stopnia wielomianu. Tym bardziej, iż w zadaniu powiedziano wyraźnie, że na rysunku widzimy tylko fragment wykresu. Przez 4 zadane punkty przechodzi dokładnie jeden wielomian stopnia nie wyższego niż 3 i nieskończenie wiele wielomianów każdego z wyższych stopni. Zadanie w oryginalnym sformułowaniu CKE nie dało się więc rozwiązać.
W zadaniu 12 sformułowanie nie wyklucza możliwości B=D, o której w schemacie rozwiązania nie ma ani słowa! Przyjęto tam milcząco, że D jest punktem wewnętrznym odcinka AB. Tym sposobem pominięto jedno z rozwiązań i należałoby za to obciąć punkty (wszak robimy to np. jeśli w rozwiązaniu równania brakuje któregoś z pierwiastków, bo standardowa konwencja w matematyce jest taka, że jeśli dane warunki spełnia kilka obiektów, w rozwiązaniu należy wymienić je wszystkie, a nie odgadnąć którys z nich).
Również opublikowane przez CKE rozwiązanie zadania 3 trudno uznać za wzorcowe. Rozwiązaniem równania kwadratowego są przecież p1 i p2, a nie "liczby jedna lub druga"!
CKE, mimo wielokrotnych monitów, konsekwentnie od trzech lat nie chce również podporządkować się podstawowym zasadom polskiej interpunkcji. Stale znajdujemy w oficjalnych dokumentach zapisy typu "2 pkt" lub "5 pkt", a przecież występujące w tych skrótach formy "punkty" i "punktów" nie kończą się na "t" i wymagają wobec tego kropki na końcu. Bez kropki piszemy jedynie "1 pkt", bo słowo "punkt" kończy się na "t". Ciekawe co na to eksperci poprawiający arkusze z języka polskiego.
Czy wiesz, kto z wrocławskich matematyków został uwiecz-niony na tym znakomitym portrecie w piżamie? Kto jest autorem tego obrazu? Gdzie można go obejrzeć?
Jako młody chłopak Knaster ożenił się z poznaną w Paryżu Marią Morską - muzą Skaman-drytów (zm. w 1945 roku). W czasach wrocła-wskich jego drugą żoną była Regina Lewandowska. Pierwszej żonie Knastera poświęcona jest książka Hanny Faryny-Paszkiewicz "Opium życia".
Steinhaus twierdził, że nazwisko Knaster brzmi w dopeł-niaczu Knastra, a sam Knaster upierał się przy formie Knastera. 
Matematyka wg CKE
Nieścisłość czy błąd? Mało istotne. To się zdarza. Ale na stronach CKE i w TV pojawiły się różne (moim zdaniem pokrętne) wyjaśnienia. Co to bowiem jest "rutynowe rozwiązanie"? Co to jest "poziom świadomości licealisty"? Co to jest "grubość kreski"? Jak na podstawie szkicu wykresu określać stopień wielomianu? Czy my przypadkiem nie zaczynamy mówić o matematyce wg CKE?
Bez szkody dla uczniów
Błąd w zad. 1 jest ewidentny. Ale nie przesadzajmy. Większość obecnych maturzystów w ogóle nigdy nie słyszała o wielomianach wyższych stopni, więc bez problemu milcząco przyjęła, że powinien on być stopnia 3.
No chyba nie jest tak źle
Myślę, że z nauczaniem matematyki nie jest aż tak tragicznie jak sugeruje ZT z ZG (a robi to także CKE w swoim komentarzu). W wielu szkołach funkcjonują przecież klasy matematyczne, gdzie młodzież wie jednak cokolwiek więcej ponad żałosną podstawę programową.
A jeśli ktoś milcząco założył w rozwiązaniu, że szukany wielomian jest stopnia 3, to powinno mu się za to obciąć punkty, bo to jest typowy dowód przez założenie tezy (zakładamy to, co należy udowodnić). Chyba że rzeczywiscie chcemy uczyć matematyki wg CKE i uznawać za pełnowartościowe - logicznie błędne rozwiązania.
Ale właśnie tych lepszych uczniów należy przed tym chronić. Powinni mieć świadomość, że w matematyce sądy są czarno-białe i albo coś jest poprawne, albo nie.
Ciekawe, jak to oceniano
Jestem bardzo ciekawa, jak oceniane były rozwiązania zad. 1 typu:
f(x) = (x+6)(x+5)(x+3)(0,000001x2- 0,000001x+1),
w zależności od dopuszczalnej "grubości kreski" liczby w ostatnim nawiasie można uczynić jeszcze mniejszymi (możecie użyć WYKRESownika z górnego paska menu i porównać wykres o podanym wzorze z oczekiwanym w zadaniu wykresem f(x) = x3+14x2+63x+90).
I co widać?
Może wypowiedzą się na ten temat jacyś tegoroczni egzaminatorzy?
Nie wolno
Im nie wolno! ABW, BOR, CBA, CIA, PKP, IPN, ITP czuwają...
Przecież się da!
Oczywiście że z fragmentu wykresu da się powiedzieć dokładnie, jaki to wielomian, bo mając fragment wykresu na dowolnym przedziale mamy dane wartości w nieskończenie wielu punktach. Stąd można już jednoznacznie wyliczyć, jaki to wielomian, wybierając pewnych n+1 punktów.
Inna sprawa, że do określenia, co to za funkcja, wystarczy znać jej własności zaledwie w jednym punkcie, a potem skorzystać z rozwinięcia w szereg Taylora.
Tyle teoria. Ale co uczeń mógłby zrobić z tą wiedzą w tym zadaniu, za diabła nie wiem.
Skandal maturalny zatacza szerokie kręgi
W czerwcowym numerze pisma dla nauczycieli "Matematyka" jeden z redaktorów tego pisma napisał o zad. 1: "oczywiście , zauważenie przez maturzystę błędu i opisanie go w rozwiązaniu będzie skutkowało przyznaniem punktów" i dalej o zad. 12: "tę niedokładność można oczywiście dość prosto zneutralizować w kluczu oceniania, dopuszczając dwie wersje odpowiedzi" - podkreślenia moje.
Ale nie ma tu nic oczywistego, a pisanie takich rzeczy jest wręcz nieprzystojne! W żadnym z tych zadań nie ma żadnych dwóch wersji odpowiedzi. Poprawne rozwiazanie jest jedno (nie da się wykazać tezy zad. 1 oraz 2 przypadki rozwiązania w zad. 12). Za błędne rozwiązania podane przez CKE jako wzorcowe powinny być uczniom odjęte punkty (no, chociaż 1 pkt). Dopuszczanie błędnych rozwiązań jako poprawnych jest fałszowaniem matematyki. To wysoka cena jak za ratowanie twarzy CKE.
Matematyka alternatywna
Dialektyka twierdzi, że ilość przechodzi w jakość. To właśnie obejrzeliśmy na tegorocznej maturze, a raczej po niej. Przy czym nie chodzi mi tutaj o to, że jedno zadanie rozwiązane źle (o wielomianie) i jedno niepełnie (o trójkącie) to nowa jakość – błędy zdarzały się zawsze i wszędzie, a ślepy los mógł umieścić dwa w jednej maturze z matematyki (obdarzając też sprawiedliwie błędami inne przedmioty).
Nie jest również niczym nadzwyczajnym pokazany w telewizji nauczyciel matematyki twierdzący, że jeśli wielomian ma trzy pierwiastki, to jest trzeciego stopnia – byłoby czymś zdumiewającym, gdyby akurat wśród nauczycieli matematyki nie było durniów.
Nadzwyczajne jest jednak oświadczenie wygłoszone w tejże telewizji przez poważnego matematyka z dorobkiem i stanowiskiem, że istnieje dodatkowy środek dowodowy: świadomość licealisty, za pomocą którego można uznać za poprawne rozumowanie w myśl "tradycyjnej" matematyki błędne.
Tak oto autor inkryminowanego zadania został uznany za twórcę matematyki alternatywnej.