Zadanie 1. Niech ABCD jest czworokątem wpisanym w okrąg o średnicy AB. Wykaż, że rzuty prostokątne boków AD i CB na prostą DC są przystające.
Zadanie 2. Niech ABCD jest czworokątem wypukłym. Rozważmy cztery okręgi, z których każdy jest styczny do trzech boków tego czworokąta. Wykaż, że ich środki są współokręgowe.
Zadanie 3. Na prostej wybrano kolejno punkty A, B, C i D tak, że |BC|=2|AB| i |CD|=|AC|. Przez punkty A i C przechodzi jeden okrąg, a drugi przez punkty B i D. Wykaż, że wspólna cięciwa tych okręgów dzieli odcinek AC na połowy.
Zadanie 4. (wolna amerykanka) Pole prostokąta ABCD wynosi 48, a długość przekątnej 10. Na płaszczyźnie dany jest punkt O taki, że |OB| = |OD| = 13. Znajdź odległość punktu O od najdalej położonego od niego wierzchołka prostokąta.
W listopadzie komplet punktów za zadania 1-3 otrzymali: Jacek Bagiński (nauczyciel matematyki w I LO Kraków), Włodzimierz Bąk (nauczyciel matematyki w I LO Opole), Iwona Gruszecka (nauczycielka matematyki w G 28 Wrocław), Anna Gudełajtis (uczennica II LO Opole), Michel Migas (student Politechniki Warszawskiej), Tadeusz Porzucek (emerytowany nauczyciel matematyki z Gostynia), Krzysztof Sobków (nauczyciel matematyki II LO Opole) i Arkadiusz Wróbel (student matematyki na UW).
Zadanie 4. poprawnie rozwiązali: Jacek Bagiński, Włodzimierz Bąk, Agnieszka Borucka (uczennica II LO Opole), Daria Bumażnik (uczennica II LO Jelenia Góra), Iwona Gruszecka, Anna Gudełajtis, Michel Migas, Tadeusz Porzucek, Krzysztof Sobków, Sabina Sy (studentka nanotechnologii na UJ), Michał Szymański (uczeń II LO Opole) i Arkadiusz Wróbel.
Po dwóch miesiącach Ligi z Geometrii Elementarnej prowadzą z 60 pkt. na 60 możliwych: Jacek Bagiński, Włodzimierz Bąk, Iwona Gruszecka, Anna Gudełajtis, Michel Migas, Krzysztof Sobków i Arkadiusz Wróbel.
W konkurencji "wolnej amerykanki" prowadzą po dwóch miesiącach: Jacek Bagiński, Włodzimierz Bąk, Daria Bumażnik, Michel Migas, Tadeusz Porzucek, Krzysztof Sobków, Sabina Sy, Michał Szymański i Arkadiusz Wróbel.
Serdecznie wszystkim gratulujemy!
Zadanie 1. Zauważmy, że czworokąt ABB'C' jest trapezem prostokątnym. Przez środek O prowadzimy prostopadłą do prostej DC. Zauważmy, że OK jest linią średnią trapezu (bo punkt K jest środkiem boku DC) i jednocześnie symetralną odcinka DC. Stąd |A'D| = |A'K| - |DK| = 1/2|A'B'| - 1/2|DC| = |KB'| - |KC| = |CB'|, co było do okazania.

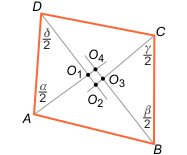
Zadanie 2. Prowadzimy dwusieczne kątów czworokąta. Przecinając się, wyznaczają one środki O1, O2, O3 i O4 odpowiednich okręgów. Zauważmy, że ∡O4O1O2 = 180° - (α/2 + δ/2) oraz ∡O4O3O2 = 180° - (β/2 + γ/2). Sumując te kąty, otrzymujemy 360° - (α+β+γ+δ)/2 = 180°, a stąd wynika teza.
Zadanie 3. Oznaczmy przez K punkt przecięcia się wspólnej cięciwy z prostą AD. Oznaczmy długość odcinka BK przez x. Stosując do obu okręgów twierdzenie o przecinających się cięciwach okręgu (patrz tutaj - dół strony), otrzymujemy równanie |FK|·|KE| = (a+x)(2a-x) = x(5a-x), którego dodatnim pierwiastkiem jest a/2. Stąd |AK| = 3/2 a, co było do okazania.

Zadanie 4. Zauważmy, że O leży na symetralnej odcinka DB. Z twierdzenia Pitagorasa w trójkącie DSO mamy |SO| = 12. Dalej rozwiązując układ równań ab = 48 i a2 + b2 = 100, otrzymujemy a=8 i b=6. Stosując twierdzenie kosinusów w trójkącie ASO, otrzymujemy
|AO|2 = |AS|2 + |SO|2 - 2·|AS|·|SO|·cos(90°+φ) = 169 +120sinφ.
Zauważmy teraz, że PASD = 12 = 25/2·sinφ, a stąd sinφ = 24/25. Podstawiając tę wartość do poprzedniego równania, otrzymujemy |AO| = 7√29/5.



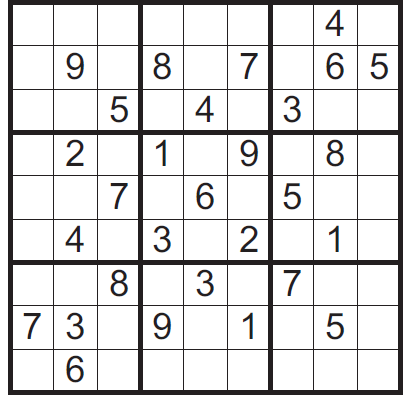
 To zabawny samouczek, który zaczynając się niewinnie intrygującą historyjką, krok po kroku, poczynając od najłatwiejszych łamigłówek, prowadzi nas w szpony, nie bójmy się użyć tego słowa, uzależnienia.
To zabawny samouczek, który zaczynając się niewinnie intrygującą historyjką, krok po kroku, poczynając od najłatwiejszych łamigłówek, prowadzi nas w szpony, nie bójmy się użyć tego słowa, uzależnienia.


