Zadanie 1. Wykaż, że w trójkącie ostrokątnym ABC (o bokach a, b, c leżących odpowiednio naprzeciw wierzchołków A, B, C) zachodzi równość |AH|·a + |BH|·b + |CH|·c = 4S, gdzie H jest ortocentrum (tzn. punktem przecięcia wysokości), a S - polem trójkąta.
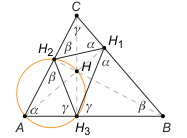
Zadanie 2. Niech O1 będzie środkiem okręgu opisanego na trójkącie BHC, gdzie H jest ortocentrum trójkąta ostrokątnego ABC. Wykaż, że O1H jest prostopadłe do H2H3, gdzie H2 i H3 są spodkami wysokości trójkąta ABC opuszczonymi odpowiednio z wierzchołków B i C.
Zadanie 3. Linia średnia w trapezie równoramiennym ma długość 5 i dzieli ten trapez na części, których pola są w stosunku 7:13. Wiadomo, że w ten trapez można wpisać okrąg. Oblicz wysokość tego trapezu.
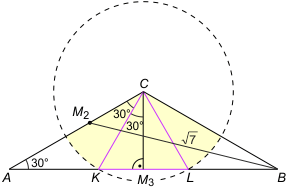
Zadanie 4. (wolna amerykanka) Kąt przy podstawie trójkąta równoramiennego ma 30°. Środkowa ramienia ma długość √7. Oblicz stosunek pola części wspólnej tego trójkąta oraz koła o promieniu 2/√3 i środku w wierzchołku naprzeciw podstawy do pola całego trójkąta.
W październikowej edycji maksymalną liczbę 30 punktów za zadania 1-3 otrzymali: Jacek Bagiński (nauczyciel matematyki, I LO Kraków), Włodzimierz Bąk (nauczyciel matematyki, I LO Opole), Agnieszka Borucka (uczennica, II LO Opole), Iwona Gruszecka (nauczycielka matematyki, G 28 Wrocław), Anna Gudełajtis (uczennica, II LO Opole), Antoni Kamiński (uczeń, III LO Wrocław), Michel Migas (student, Warszawa), Krzysztof Sobków (nauczyciel matematyki, II LO Opole), Sabina Sy (studentka nanotechnologii na UJ, Kraków), Arkadiusz Wróbel (student UW, Warszawa). Natomiast Tadeusz Porzucek (emerytowany nauczyciel matematyki z Gostynia) uzyskał 28 pkt. Gratulacje!
Zadanie 4 poprawnie rozwiązali: Jacek Bagiński, Włodzimierz Bąk, Daria Bumażnik (uczennica, II LO Jelenia Góra), Teresa Chmielewska (specjalista d/s technicznych, Wrocław), Michel Migas, Krzysztof Sobków, Michał Szymański (uczeń, II LO Opole), Sabina Sy, Tadeusz Porzucek i Arkadiusz Wróbel. Gratulacje!
Zadanie 1. Rozważmy trójkąt A'B'C' o bokach równoległych do boków trójkąta ABC i przechodzących przez jego wierzchołki. Jest on podobny (z cechy kkk) do wyjściowego trójkąta w skali 2 (dlaczego takiej?), a jego pole wynosi 4S, gdzie S jest polem trójkąta ABC. Zauważmy, że pole trójkąta A'B'C' jest sumą pól trójkątów A'HB', B'HC' oraz C'HA'. Stąd mamy 4S = PA'B'C' = 1/2·|A'B'|·|CH| + 1/2·|B'C'|·|AH| + 1/2·|C'A'|·|BH| = AB|·|CH| + |BC|·|AH| + |AC|·|BH| = a·|AH| + b·|BH| + c·|CH|.

Zadanie 2. Skorzystajmy z faktu, że odcinek H2H3 jest antyrównoległy do BC, tzn. ∡AH2H3 = β i ∡AH3H2 = γ (co można łatwo udowodnić - patrz niżej). Poprowadźmy styczną l do okręgu w punkcie H. Wystarczy wykazać, że jest ona równoległa do H2H3 (bo jest prostopadła do promienia O1H). Zauważmy, że kąt dopisany PHC ma miarę taką, jak kąt HBC (wpisany w okrąg, oparty na tym samym łuku), a ten z kolei jak kąt H2BC = 90°-γ. Tymczasem kąt PCH ma miarę taką, jak kąt H2CH, a ten z kolei taką, jak kąt ACH3=90°-α. Zatem kąt H2PH jako kąt zewnętrzny trójkąta PHC ma miarę 90°-γ+90-α = β, a to dowodzi równoległości stycznej l i odcinka H2H3. Stąd wynika już teza.

Antyrównoległość. Proste l1 i l2 są antyrównoległe (względem prostych m1 i m2), jeśli kąty między tymi prostymi spełniają zależność z rysunku b) poniżej.

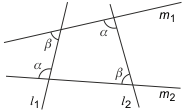
a) proste równoległe b) proste antyrównoległe
Twierdzenie o trójkącie spodkowym. Boki trójkąta spodkowego (łączące spodki wysokości trójkąta ABC) są antyrównoległe do boków wyjściowego trójkąta.
Dowód. Pokażemy, że H2H3 jest antyrównoległe do BC (pozostałe analogicznie).
Zauważmy, że na czworokącie AH3HH2 można opisać okrąg (kąty proste przy H2 i H3). Wówczas kąty AH2H3 i AHH3 są przystające (jako wpisane oparte na tym samym łuku), a ich wspólna miara (z trójkąta prostokątnego AHH3) wynosi 90°- |∡HAH3|, co z kolei (z trójkąta prostokątnego ABH1) jest równe 90° - (90°-β) = β. I dalej |∡AH3H2| = γ (z sumy kątów trójkąta AH3H2), c.b.d.o.
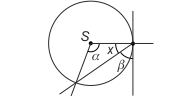
Kąt dopisany do okręgu. Kąt o wierzchołku na okręgu, którego ramionami są styczna do okręgu w wierzchołku kąta i dowolna cięciwa.

Twierdzenie o kącie dopisanym. Kąt dopisany do okręgu jest dwa razy mniejszy od kąta środkowego opartego na tym samym łuku (czyli równy kątowi wpisanemu w okrąg opartemu na tym samym łuku).
Dowód. Zachodzi α+2x = 180° (suma kątów trójkąta) oraz β+x = 90° (prostopadłość promienia do stycznej). Stąd α=2β.
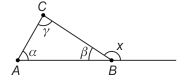
Twierdzenie o kącie zewnętrznym trójkąta. Kąt zewnętrzny trójkąta ma miarę równą sumie miar kątów wewnętrznych do niego nieprzyległych.
Dowód. Zachodzi x = 180°-β = 180°-(180°-α-γ) = α+γ.
Zadanie 3. Przy oznaczeniach jak na rysunku otrzymujemy układ równań a+b=10 (bo linia średnia wynosi 5) oraz (5+b)/(a+5)=7/13. Rozwiązaniem tego układu jest para (8, 2), czyli |AK|=3. Wobec założenia o wpisywalności okręgu i równoramienności trapezu otrzymujemy |AD|+|BC| = a+b = 10, czyli |AD|=|BC|=5. Z twierdzenia Pitagorasa w trójkącie AKD otrzymujemy |DK|=4.

Zadanie 4. Zanim wykonamy rysunek, trzeba porównać długości promienia i wysokości opuszczonej z wierzchołka C. Z twierdzenia kosinusów w trójkącie ABM2 otrzymujemy 7 = |AM2|2 + |AB|2 - 2·|AM2|·|AB|·cos30°. Zauważmy, że |AM3| = 2|AM2|·√3/2 (boki w trójkącie prostokątnym AM3C). Zatem |AB| = |AM2|·√3. Po podstawieniu do równania otrzymujemy |AM2| = 1, zatem |AC| = 2. Stąd |CM3| = 1 (przyprostokątna naprzeciw kąta 30°). Wynika stąd, że promień koła jest większy niż wysokość i część wspólna z trójkątem ABC jest sumą trójkąta KLC oraz dwóch wycinków koła. Rozważmy teraz trójkąt prostokątny CKM3. Zachodzi |CM3|/|CK| = √3/2 = cos∡KCM3. Wynika stąd, że |∡KCM3| = 30°. Z symetrii wnioskujemy, że trójkąt KLC jest równoboczny, a wycinki koła mają kąt rozwarcia 30°. Zatem pole części wspólnej wynosi 2·π/12·(2/√3)2 + (2/√3)2· √3/4 = (2π+3√3)/9. Ponieważ pole trójkąta ABC wynosi √3, otrzymujemy szukany stosunek pól wynoszący (2√3π+9)/27.


 To zabawny samouczek, który zaczynając się niewinnie intrygującą historyjką, krok po kroku, poczynając od najłatwiejszych łamigłówek, prowadzi nas w szpony, nie bójmy się użyć tego słowa, uzależnienia.
To zabawny samouczek, który zaczynając się niewinnie intrygującą historyjką, krok po kroku, poczynając od najłatwiejszych łamigłówek, prowadzi nas w szpony, nie bójmy się użyć tego słowa, uzależnienia.



Definicja wolnej amerykanki
Jeśli dobrze rozumiem, można wsunąć nieelementarne metody.
Definicja
Wszystko wyjaśnione jest w regulaminie Ligi.