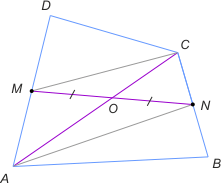
Zad. 1. Wewnątrz wielokąta wypukłego dane są różne punkty P i Q. Wykaż, że istnieje wierzchołek od którego bliżej jest do punktu Q niż do P.
Zad. 2. W czworokącie wypukłym ABCD punkty M i N są środkami przeciwległych boków AD i BC. Przekątna AC przechodzi przez środek odcinka MN. Oblicz pole czworokąta ABCD, jeśli pole trójkąta ABC wynosi S.
Zad. 3. Niech BK będzie dwusieczną kąta w trójkącie równoramiennym (|AB|= |AC|). Wykaż, że |BK| < 2|CK|.
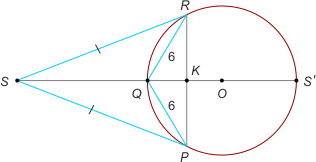
Zad. 4. (wolna amerykanka) Pole czworokąta PQRS wynosi 48. Wiadomo, że |PQ| = |QR| = 6, |RS| = |SP|, a wierzchołki P, Q, R (i tylko one) leżą na okręgu o promieniu 5. Znajdź długość boków RS i SP.
Zapraszamy do zgłaszania się na XVI Mistrzostwa Polski w Geometrii Elementarnej. Zawody odbędą się 9 VI we Wrocławiu (i równolegle na obozie olimpijskim w Mszanie Dolnej).
Za zadania 1-3 punkty zdobyli:
- 30 pkt. -Jacek Bagiński (nauczyciel matematyki, I LO Kraków), Włodzimierz Bąk (nauczyciel akademicki UO), Szymon Kaźmierowski (nauczyciel, IV LO Elbląg), Michel Migas (student matematyki PW), Tadeusz Porzucek (emerytowany nauczyciel, Gostyń), Dominik Sulik (uczeń, I LO Kraków) i Adrianna Bodziony (uczennica, I LO Kraków),
- 20 pkt. - Ewa Dobrowolska (uczennica, III LO Wrocław).
W kategorii wolnej amerykanki punkty zdobyli:
- 10 pkt. - Włodzimierz Bąk, Zygmunt Krawczyk (nauczyciel, SLO Żary), Michel Migas, Dominik Sulik i Adrianna Bodziony,
- 8 pkt. - Jacek Bagiński,
- 2 pkt. - Ewa Dobrowolska i Tadeusz Porzucek.
Gratulujemy!
Zad. 1. Załóżmy, że nie ma takiego wierzchołka. Oznacza to, że wszystkie wierzchołki leżą na półpłaszczyźnie wyznaczonej przez symetralną odcinka PQ po tej stronie co P. Zatem punkt Q musiałby leżeć poza wielokątem, co daje sprzeczność.
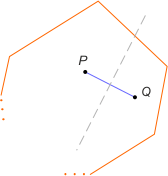
Zad. 2. Zachodzi PΔ MOC = PΔCON oraz PΔMAO = PΔAON, bo O jest środkiem odcinka MN. Wynika stąd, że PΔAMC = PΔANC. Z kolei PΔDMC = PΔAMC = PΔANC = PΔABN (z definicji punktów M i N). Zatem PΔACD = PΔABC = S. Ostatecznie PABCD = 2S.
Zad. 3. Poprowadźmy przez K prostą równoległą do BC przecinającą bok AB w punkcie E. Zauważmy, że |∡BKE| = β/2 (kąty naprzemianległe). Zatem trójkąt BEK jest równoramienny, przy czym |KE| = |EB|. Z drugiej strony czworokąt EBCK jest trapezem równoramiennym i |EB| = |CK|. Z nierówności trójkąta otrzymujemy |BK| < |KE|+|EB| = 2|CK|.
Zad. 4. (wolna amerykanka) Z założenia punkty Q i S leżą na symetralnej odcinka PR i prosta QS przechodzi przez środek okręgu. Rozważmy przypadek gdy Q i S leżą po różnych stronach odcinka PR. Niech QS' jest średnicą okręgu. Wówczas kąt QRS' jest prosty i z twierdzenia Pitagorasa dla trójkąta QRS' otrzymujemy |S'R| = 8. Wiemy, że pole czworokąta PS'RQ wynosi 48. Oznacza to, że punkt S pokrywa się z S'. Przeczy to założeniu, że S nie leży na okręgu. Rozważmy zatem przypadek, gdy punkty Q i S leżą po jednej stronie odcinka PR. Wówczas RK jest wysokością trójkąta QS'R i wynosi 4,8 zatem |PR| = 9,6. Wobec założenia PPQRS = 48, mamy |SQ| = 10. W trójkącie QKR mamy cos(∡RQK) = 3/5. Z twierdzenia kosinusów dla trójkąta SQR mamy |SR|2 = |SQ|2 + |QR|2 – 2|SQ|·|QR|·cos(∡SQR) = 100 + 36 – 2·10·6·(-3/5) = 208. Ostatecznie |SR| = |SP| = √208 = 4√13.
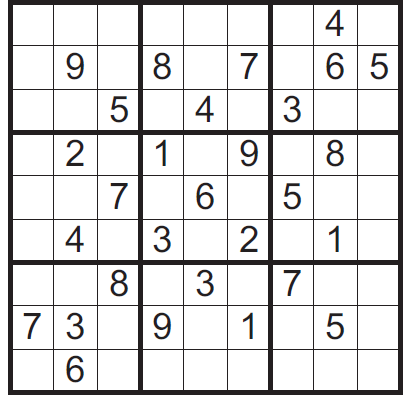
To zabawny samouczek, który zaczynając się niewinnie intrygującą historyjką, krok po kroku, poczynając od najłatwiejszych łamigłówek, prowadzi nas w szpony, nie bójmy się użyć tego słowa, uzależnienia.
