Zad. 1. W trójkąt o obwodzie 2p wpisano okrąg i poprowadzono styczną równoległą do jednego boku. Znaleźć możliwie największą długość odcinka tej stycznej ograniczonego bokami trójkąta.
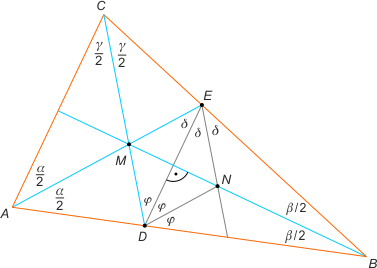
Zad. 2. Niech AE i CD będą dwusiecznymi w trójkącie ABC. Wykaż, że jeśli |∡BDE| : |∡EDC| = |∡BED| : |∡DEA|, to trójkąt ABC jest równoramienny.
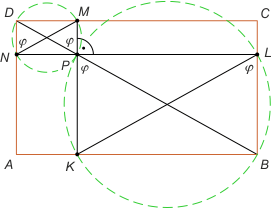
Zad. 3. Na bokach AB, BC, CD i DA prostokąta ABCD obrano odpowiednio punkty K, L, M i N różne od wierzchołków. Wiedząc, że KL i MN są równoległe, a KM i NL prostopadłe, wykaż, że punkt wspólny odcinków KM i LN leży na przekątnej BD.
Zad. 4. (wolna amerykanka) Wykaż, że w trójkącie ABC prawdziwa jest nierówność: |AB|2 + |BC|2 + |CA|2 ≤ 9R2, gdzie R jest promieniem okręgu opisanego na trójkącie ABC.
Za zadania 1-3 punkty zdobyli:
- 30 pkt - Włodzimierz Bąk (nauczyciel akademicki UO), Jacek Bagiński (nauczyciel matematyki, I LO Kraków), Michel Migas (student matematyki PW), Dominik Sulik (uczeń, I LO Kraków),
- 20 pkt. - Szymon Kaźmierowski (nauczyciel, IV LO Elbląg) oraz Tadeusz Porzucek (emerytowany nauczyciel, Gostyń).
W 'wolnej amerykance' 10 pkt. zdobyli: Jacek Bagiński, Włodzimierz Bąk, Zygmunt Krawczyk (nauczyciel, SLO Żary), Michel Migas, Tadeusz Porzucek, Dominik Sulik i Szymon Kaźmierowski. Gratulacje!
Zapraszamy do zgłaszania się na XVI Mistrzostwa Polski w Geometrii Elementarnej. Zawody odbędą się 9 VI we Wrocławiu (i równolegle na obozie olimpijskim w Mszanie Dolnej).
Zad. 1. Zauważmy, że trójkąty KLB i ABC są podobne (kkk), stąd stosunek ich obwodów równy jest skali podobieństwa. Otrzymujemy zatem równość: x/b = (2p–2b)/2p, gdzie 2p–2b stanowi obwód trójkąta KLB. Po przekształceniach otrzymujemy x = -b2/p + b. Największą wartość wyrażenie to przyjmuje dla b = p/2 i wynosi ona p/4.
Zad. 2. Niech |∡BDE| : |∡EDC| = |∡BED| : |∡DEA| = k. Wówczas |∡EDC| = |∡BDE|/k oraz |∡DEA| = |∡BED|/k. Zauważmy, że |∡DME| = 90° + β/2. Z twierdzenia o sumie kątów wewnetrznych dla trójkąta DME otrzymujemy 180° = 90° + β/2 + (|∡BDE| + |∡BED|)/k = 90° + β/2 + (180°–β)/k, skąd po przekształceniach mamy (180°–β)/2 = (180°–β)/k. Zatem k=2. Niech N będzie punktem przecięcia dwusiecznych kątów trójkąta DBE. Oczywiście N leży na dwusiecznej BM. Wystarczy zatem wykazać, że BM jest prostopadła do DE. Niech |∡MDE| = φ oraz |∡MED| = δ. Zachodzi |∡MDE| = |∡EDN| = |∡NDB| = φ oraz |∡MED| = |∡DEN| = |∡NEB| = δ. Punkt N jest obrazem punktu M w symetrii względem DE, czyli MN jest prostopadłe do DE. Ponieważ BN jest dwusieczną kąta DBE, to trójkąt DBE jest równoramienny, przy czym |DB| = |EB| oraz φ = δ. Ostatecznie trójkąty AEB i CDB są przystające (kbk), a stąd |AB| = |BC|.
Zad. 3. Z założenia |∡KLB| = |∡DNM| = φ, bo odpowiednie ramiona tych kątów są równoległe. Na czworokątach NPMD oraz KBLP można opisać okręgi (suma kątów przeciwległych wynosi 180°), zatem |∡DPM| = φ oraz |∡KPB| = φ (kąty wpisane oparte na tych samych łukach co kąty DNM i KLB). Z równości kątów DPM i KPB (jako wierzchołkowych) wynika teza.
Zad. 4. (wolna amerykanka) Niech O będzie środkiem okręgu opisanego na trójkacie, a α, β, γ - miarami kątów trójkąta.Zastosujemy metodę wektorową. Zauważmy, że AB = OB–OA, BC = OC–OB oraz CA = OA–OC. Zatem |AB|2 + |BC|2 + |CA|2 = AB2 + BC2 + CA2 = (OB–OA)2 + (OC–OB)2 + (OA–OC)2 = OB2 – 2·OB•OA + OA2 + OC2 – 2·OC•OB + OB2 + OA2 – 2·OC•OA + OC2 = 6R2 – 2R2(cos2γ+cos2α+cos2β). Z drugiej strony (OA+OB+OC)2 ≥ 0. Po podniesieniu do kwadratu otrzymujemy 3R2 + 2R2(cos2α+cos2β+cos2γ) ≥ 0, skąd cos2α + cos2β + cos2γ ≥ -3/2, a po podstawieniu tej wartości do poprzedniego równania otrzymujemy tezę.
Czy wiesz, kto z wrocławskich matematyków został uwiecz-niony na tym znakomitym portrecie w piżamie? Kto jest autorem tego obrazu? Gdzie można go obejrzeć?
Jako młody chłopak Knaster ożenił się z poznaną w Paryżu Marią Morską - muzą Skaman-drytów (zm. w 1945 roku). W czasach wrocła-wskich jego drugą żoną była Regina Lewandowska. Pierwszej żonie Knastera poświęcona jest książka Hanny Faryny-Paszkiewicz "Opium życia".
Steinhaus twierdził, że nazwisko Knaster brzmi w dopeł-niaczu Knastra, a sam Knaster upierał się przy formie Knastera. 
