Zad. 1. Okrąg wpisany w trójkąt ABC jest styczny do boków AB i AC odpowiednio w punktach N i M. Dwusieczna kąta B przecina MN w punkcie K. Wykaż, że kąt BKC jest prosty.
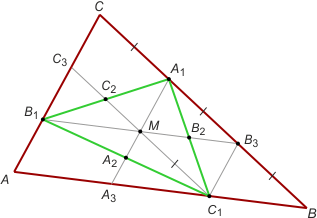
Zad. 2. Na bokach BC, CA i AB trójkąta ABC obrano odpowiednio punkty A1, B1 i C1 tak, że środkowe A1A2, B1B2 i C1C2 trójkąta A1B1C1 są równoległe do odpowiednich boków trójkąta ABC. W jakim stosunku punkty A1, B1 i C1 dzielą boki trójkąta ABC?
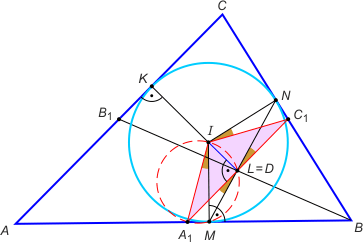
Zad. 3. W trójkąt ABC wpisano okrąg styczny do boków AC, AB i BC odpowiednio w punktach K, M i N. Środkowa BB1 przecina odcinek MN w punkcie D. Wykaż, że środek okręgu leży na prostej DK.
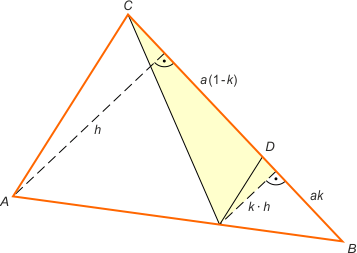
Zad. 4. (wolna amerykanka) W trójkącie ABC o polu 8 poprowadzono równolegle do boku AC odcinek DE. Pole trójkąta DEC wynosi 2. Oblicz stosunek DE do AC.
Za zadania 1-3 punkty zdobyli:
30 pkt - Włodzimierz Bąk (nauczyciel akademicki UO), Michel Migas (student matematyki PW), Dominik Sulik (uczeń, I LO Kraków)
22 pkt. Tadeusz Porzucek (emerytowany nauczyciel, Gostyń)
20 pkt. - Ewa Dobrowolska (uczennica, III LO Wrocław), Jacek Bagiński (nauczyciel matematyki, I LO Kraków), Szymon Kaźmierowski (nauczyciel, IV LO Elbląg)
W kategorii wolnej amerykanki 10 pkt. zdobyli:
Jacek Bagiński, Włodzimierz Bąk, Zygmunt Krawczyk (nauczyciel, SLO Żary), Michel Migas, Tadeusz Porzucek, Dominik Sulik, Szymon Kaźmierowski
Gratulacje
Zad. 1. Zauważmy, że |∡BIC| = 90° + α/2, bo BI i CI są dwusiecznymi. Zatem |∡KIC| = 90° – α/2 (przyległy do kąta BIC). Z drugiej strony w trójkącie równoramiennym ANM mamy |<AMN| = 90° – α/2. Oznacza to, że na czworokącie CMKI można opisać okrąg o średnicy CI. Stąd teza.
Zad. 2. Niech M oznacza środek ciężkości trójkąta A1B1C1. Z założenia B1B3 jest równoległe do AB oraz B2 jest środkiem A1C1, więc B2B3 jest linią średnią w trójkącie A1C1B. Stąd |BB3| = |B3A1|. Również z założenia czworokąt MC1BB3 jest równoległobokiem. Wobec tego czworokąt MC1B3A1 jest też równoległobokiem. Jego przekątne się połowią, więc |B3B2| = |B2M|. Oznacza to, że M jest środkiem odcinka B1B3, a MA1 jest linią średnią w trójkącie B1B3C. Stąd |A1C| = |B3A1|= |BB3|. Ostatecznie punkt A1 dzieli bok BC w stosunku 2:1. Pozostałe punkty analogicznie.
Zad. 3. Niech L będzie punktem wspólnym prostych MN i KI. Poprowadźmy przez niego prostą równoległą do boku AC, przecinającą boki AB i BC odpowiednio w punktach A1 i C1. Wystarczy wykazać, że |A1L| = |LC1|. Będzie to oznaczało, że L leży na środkowej BB1 i pokrywa się z punktem D. Zauważmy, że kąty A1MI oraz A1LI są proste, więc na czworokącie A1MLI można opisać okrąg. Analogicznie czworokąt ILC1N jest wpisywalny w okrąg. Mamy zatem |∡A1IM| = |∡A1LM| = |∡NLC1| = |∡NIC1|. Równość skrajnych kątów oznacza, że trójkąty prostokątne A1MI oraz NIC1 są przystające, a |IC1| = |IA1|. Z kolei IL jest wysokością w trójkącie równoramiennym A1C1M i dzieli odcinek A1C1 na połowy. Stąd teza.
Zad. 4. (wolna amerykanka) Oznaczmy skalę podobieństwa trójkątów EBD i ABC przez k. Wówczas BD = k·a oraz |DC| = (1–k)·a. Otrzymujemy PΔDEC = k·h·a·(1–k)/2 = PΔABC·k·(1–k).
Podstawiając dane, otrzymujemy równanie 2 = 8·k·(1–k), skąd k = 1/2.
Czy wiesz, kto z wrocławskich matematyków został uwiecz-niony na tym znakomitym portrecie w piżamie? Kto jest autorem tego obrazu? Gdzie można go obejrzeć?
Jako młody chłopak Knaster ożenił się z poznaną w Paryżu Marią Morską - muzą Skaman-drytów (zm. w 1945 roku). W czasach wrocła-wskich jego drugą żoną była Regina Lewandowska. Pierwszej żonie Knastera poświęcona jest książka Hanny Faryny-Paszkiewicz "Opium życia".
Steinhaus twierdził, że nazwisko Knaster brzmi w dopeł-niaczu Knastra, a sam Knaster upierał się przy formie Knastera. 
