Zad. 1. Na prostej l zaznaczono różne punkty A i B. Znajdź zbiór punktów styczności par okręgów, które będąc wzajemnie styczne, są też styczne do prostej l, jeden w punkcie A, a drugi w B.
Zad. 2. Dane są trzy okręgi o promieniu r mające jeden punkt wspólny. Każdy z nich jest styczny do dwóch boków trójkąta ABC. Promień okręgu opisanego na tym trójkącie wynosi R. Oblicz promień okręgu wpisanego w ten trójkąt.
Zad. 3. Przez końce średnicy CD poprowadzono styczne do okręgu. Prosta l styczna do okręgu przecina te styczne odpowiednio w punktach A i B. Wykaż, że wielkość |AC|·|BD| nie zależy od położenia stycznej l.
Zad. 4. (wolna amerykanka) W trójkącie prostokątnym wysokość opuszczona na przeciwprostokątną dzieli ją na dwa odcinki, których długości różnią się o długość jednej z przyprostokątnych. Znajdź kąty tego trójkąta.
Za zadania 1-3 punkty zdobyli: 30 pkt - Włodzimierz Bąk (nauczyciel akademicki UO), Michel Migas (student matematyki PW) i Tadeusz Porzucek (emerytowany nauczyciel, Gostyń), Jacek Bagiński (nauczyciel matematyki, I LO Kraków), Szymon Kaźmierowski (nauczyciel, IV LO Elbląg), Dominik Sulik (uczeń, I LO Kraków) oraz Ewa Dobrowolska (uczennica, III LO Wrocław), 10 pkt. - Tomasz Szczepanik (uczeń, I LO Kraków).
W kategorii wolnej amerykanki 10 pkt. zdobyli: Jacek Bagiński, Włodzimierz Bąk, Zygmunt Krawczyk (nauczyciel, SLO Żary), Michel Migas, Tadeusz Porzucek, Dominik Sulik, Szymon Kaźmierowski, Tomasz Szczepanik oraz Ewa Dobrowolska (witamy nową zawodniczkę!).
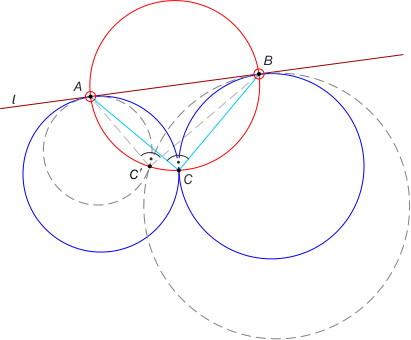
Zad. 1. Łatwo wykazać, że kąty ACB i AC'B są proste. Szukanym zbiorem punktów jest okrąg o średnicy AB bez punktów A i B.
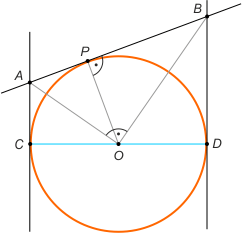
Zad. 2. Kąt AOB jest prosty, bo OA i OB są dwusiecznymi kątów, których suma miar wynosi 180°. Z własności wysokości opuszczonej na przeciwprostokątną mamy R2 = |OP|2 = |AP|·|PB| = |AC|·|BD|. Stąd wynika teza.
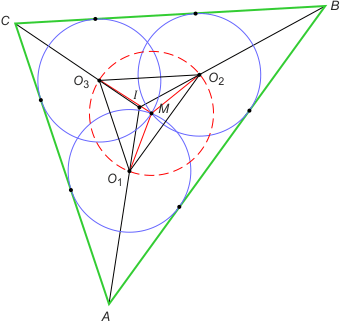
Zad. 3. Niech M oznacza punkt wspólny okręgów. Z równości |MO1| = |MO2| = |MO3| = r wynika, że M jest środkiem okręgu opisanego na trójkącie O1O2O3. Boki trójkąta O1O2O3 są równoległe do boków trójkąta ABC (odległość między nimi wynosi r). Wynika stąd podobieństwo tych trójkątów (kkk) oraz pokrywanie się środków okręgów wpisanych w te trójkąty. Niech rx oznacza szukany promień. Otrzymujemy równość rx/R = (rx – r)/r, skąd rx = Rr/(R–r).
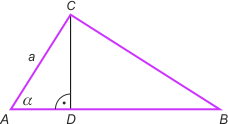
Zad. 4. (wolna amerykanka) Przy przyjętych oznaczeniach mamy |AD| = acosα, |DB| = a(1+cosα), |BC| = atgα oraz |AB| = a(1+2cosα). Z twierdzenia Pitagorasa otrzymujemy równanie 1 + tg2 α = (1+2cosα)2, którego jedynym rozwiązaniem spełniającym warunki zadania jest α = 30°. Szukane miary kątów trójkąta to 30°, 60° i 90°.
Czy wiesz, kto z wrocławskich matematyków został uwiecz-niony na tym znakomitym portrecie w piżamie? Kto jest autorem tego obrazu? Gdzie można go obejrzeć?
Jako młody chłopak Knaster ożenił się z poznaną w Paryżu Marią Morską - muzą Skaman-drytów (zm. w 1945 roku). W czasach wrocła-wskich jego drugą żoną była Regina Lewandowska. Pierwszej żonie Knastera poświęcona jest książka Hanny Faryny-Paszkiewicz "Opium życia".
Steinhaus twierdził, że nazwisko Knaster brzmi w dopeł-niaczu Knastra, a sam Knaster upierał się przy formie Knastera. 
