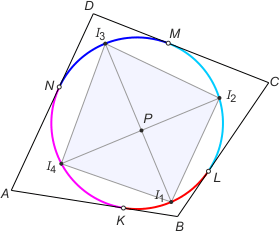
Zad. 1. Czworokąt ABCD opisano na okręgu. Punkty styczności okręgu z bokami AB, BC, CD i DA oznaczmy odpowiednio przez K, L, M, i N. Wykazać, że przekątne czworokąta, którego wierzchołkami są środki okręgów wpisanych w trójkąty KBL, LCM, MDN i NAK, są prostopadłe.
Zad. 2. Wierzchołki trójkąta dzielą okrąg na nim opisany na trzy łuki. Wykazać, że okręgi, których środkami są środki tych łuków i które przechodzą przez dwa wierzchołki trójkąta, mają wspólny punkt.
Zad. 3. Na bokach trójkąta jako na średnicach zbudowano okręgi. Odcinki wspólnych stycznych zewnętrznych (między punktami styczności) mają długości m, n i k. Oblicz pole i obwód trójkąta.
Zad. 4. (wolna amerykanka) W trójkącie ostrokątnym ABC z wierzchołków A i C opuszczono wysokości AD i CE. Wiadomo, że |DE| = 2√2, pole trójkąta ABC wynosi 18, a trójkąta BDE - 2. Oblicz promień okręgu opisanego na trójkącie ABC.
W Nowym Roku życzę wszystkim satysfakcji z rozwiązywania kolejnych zadań.
Oto wyniki za grudzień. Zadania okazały się trochę trudniejsze. Za zadania 1 - 3 punkty zdobyli:
- 30 pkt. - Włodzimierz Bąk (nauczyciel akademicki UO) oraz Michel Migas (student matematyki PW),
- 20 pkt. - Jacek Bagiński (nauczyciel matematyki, I LO Kraków), Tadeusz Porzucek (emerytowany nauczyciel, Gostyń) oraz Dominik Sulik (uczeń, I LO Kraków).
Za "wolną amerykankę" 10 pkt. zdobyli: JacekBagiński, Włodzimierz Bąk, Michel Migas, Zygmunt Krawczyk (nauczyciel, SLO Żary), Tadeusz Porzucek oraz Dominik Sulik.
Gratulacje!
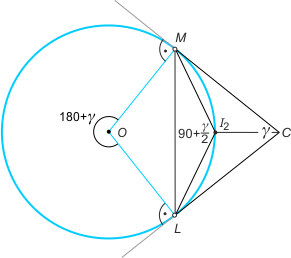
Zad. 1. Rozważmy trójkąt LCM. Niech I2 oznacza środek okręgu wpisanego. Wówczas |∡MI2L| = 90°+γ/2. Z drugiej strony kąt środkowy wklęsły oparty na łuku ML wyjściowego okręgu ma miarę 180°+γ, co oznacza, że punkt I2 leży na wyjściowym okręgu. Analogicznie środki okręgów wpisanych w trójkąty KBL, MDN i NAK także leżą na tym okręgu. Zauważmy teraz, że kąt między cięciwami I1I3 oraz I2I4 jest równy sumie kątów wpisanych opartych na łukach, których suma jest połową okręgu. Stąd wynika teza.
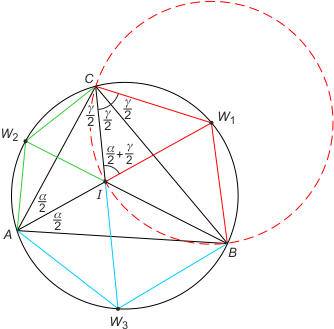
Zad. 2. Niech I oznacza środek okręgu wpisanego w trójkąt ABC, a W1 środek łuku BC. Wówczas AW1 jest dwusieczną kąta A. Odcinek CI zawiera się w dwusiecznej kąta C. Mamy wówczas |∡CIW1|= α/2 + γ/2 (z właśności kąta zewnętrznego trójkata AIC) oraz |∡ICW1| = α/2 + γ/2, co oznacza, że trójkąt CIW1 jest równoramienny i CW1 ≡ IW1. Z drugiej strony CW1 ≡ BW1 (to cięciwy, na których opierają się kąty o mierze α/2). Mamy zatem W1C ≡ W1I ≡ W1B. Oznacza to, że środek I leży na okręgu o środku W1 przechodzącym przez wierzchołki B i C. Analogicznie jest dla trójkątów W2AC i W3AB. Oznacza to, że wspólnym punktem podmiotowych okręgów jest I.
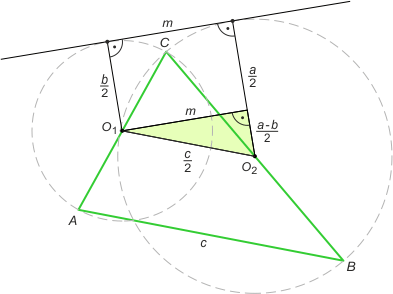
Zad. 3. Rozważmy jedną parę okręgów. Stosując twierdzenie Pitagorasa i proste przekształcenia, otrzymamy 4m2 = c2 – (a–b)2 = (c–a+b)(c+a–b) = 4(p–a)(p–b), a stąd m2 = (p–a)(p–b), gdzie p oznacza połowę długości obwodu trójkąta ABC. Analogicznie dla pozostałych par okręgów mamy n2 = (p–c)(p–a) oraz k2 = (p–c)(p–b). Po wymnożeniu tych równań stronami otrzymujemy mnk = (p–a)(p–b)(p–c). Z kolei k2m2/n2 = (p–b)2, skąd p–b = km/n. Dalej k2n2/m2 = (p–c)2, skąd p–c = kn/m oraz m2n2/k2 = (p–a)2, skąd p–a = mn/k. Dodając stronami ostatnie trzy równania, otrzymujemy p = km/n + kn/m + mn/k. Ostatecznie szukany obwód wynosi 2(k2m2 + k2n2 + m2n2)/nmk, a pole √[p(p–a)(p–b)(p–c)] = √(k2m2 + k2n2 + m2n2).
Zad. 4. (wolna amerykanka) Można wykazać (zadanie 2, październik 2014), że trójkąt EBD jest podobny do wyjściowego w skali k = √(SEBD/SABC) = 1/3. Zauważmy, że k = |EB|/|BC| = cosβ. Stąd cosβ = 1/3, a sinβ = 2√2/3. Z twierdzenia sinusów w trójkącie EDB mamy |ED|/sinβ = 2r, gdzie r jest długością promienia okręgu opisanego na trójkącie EDB. Stąd r = 3/2. Ostatecznie ze skali podobieństwa wynika, że szukany promień okręgu opisanego na trójkącie ABC wynosi 9/2.
Czy wiesz, kto z wrocławskich matematyków został uwiecz-niony na tym znakomitym portrecie w piżamie? Kto jest autorem tego obrazu? Gdzie można go obejrzeć?
Jako młody chłopak Knaster ożenił się z poznaną w Paryżu Marią Morską - muzą Skaman-drytów (zm. w 1945 roku). W czasach wrocła-wskich jego drugą żoną była Regina Lewandowska. Pierwszej żonie Knastera poświęcona jest książka Hanny Faryny-Paszkiewicz "Opium życia".
Steinhaus twierdził, że nazwisko Knaster brzmi w dopeł-niaczu Knastra, a sam Knaster upierał się przy formie Knastera. 
Rozwiązanie nieelementarne
Rozwiązanie zad. 3. trudno jest uznać za elementarne, skoro używa wzoru Herona na pole trójkąta. To jest fakt z zakresu trygonometrii (do dowodu potrzebne jest twierdzenie kosinusów).
Niekoniecznie
Do dowodu wzoru Herona wystarczą: twierdzenie Pitagorasa, klasyczny wzór na pole trójkąta i nieco przekształceń. W żadnym wypadku nie jest potrzebna trygonometria (patrz np. https://en.wikipedia.org/wiki/Heron%27s_formula#Algebraic_proof_using_th... ).