POPULARYZACJA. Jest to książka dla laików zainteresowanych matematyką prezentująca w przystępny sposób dowody 30 faktów matematycznych z różnych działów, m.in. niewymierność liczb √2 i e, rozbieżność szeregu harmonicznego i odwrotności liczb pierwszych, nieprzeliczalność zbioru liczb rzeczywistych, twierdzenia Pitagorasa i Talesa, sinusów i kosinusów itd. W książce zaprezentowano trzy podstawowe typy dowodów: wprost, nie wprost oraz indukcyjne.
Jak tego dowieść - krótka opowieść
Okruchy matematyki
POPULARYZACJA. Zbiór miniatur matematycznych dotyczących słynnych i mniej znanych problemów z zakresu geometrii, topologii i arytmetyki, rozwiązanych i takich, na które matematycy nie znaleźli jeszcze odpowiedzi. Zostały one opowiedziane bez specjalistycznych formalizmów, ale i bez spłycających ideę problemu uproszczeń. Artykuły zebrane są w trzech częściach wymagających od czytelnika coraz wyższej kultury matematycznej. Część pierwsza jest dostępna dla gimnazjalistów, część ostatnia wymaga poziomu rozszerzonej matury.
Logika popularna. Przystępny zarys logiki zdań
POPULARYZACJA. Podręcznik poprawnego wyrażania myśli w formie zdań logicznych oraz sprawnego rozumowania, czyli wysnuwania wniosków z przesłanek. Tłumaczy, czym zajmuje się logika (m.in. czym różnią się zdania i spójniki logiczne od zdań i spójników językowych), jakie są jej reguły oraz zastosowania w matematyce i poza nią (np. w technice i naukach humanistycznych). Znając podstawowe prawa logiki, można łatwo analizować poprawność wnioskowań i znajdować w nich błędy. Książka pozwala gruntownie odświeżyć, poszerzyć i uporządkować szkolną wiedzę z tego zakresu.
Królowa bez Nobla
POPULARYZACJA. Podtytuł książki brzmi "Rozmowy o matematyce", więc jak w każdej rozmowie, tak i w tej książce nie mogło zabraknąć pytań - czasem oczywistych, a czasem zaskakujących, oraz dowcipnych i frapujących odpowiedzi. Autorzy znani są zresztą z poczucia humoru, stąd nie brak w książce anegdot i żartów rysunkowych. Całość można polecić zarówno pasjonatom matematyki jak i zadeklarowanym humanistom, a przede wszystkim nauczycielom.
Bezmiar matematycznej wyobraźni
POPULARYZACJA. Wstęga Möbiusa, dywan Sierpińskiego, butelka Kleina – to pojęcia, które dla wielu uczniów brzmią egzotycznie i wydają się bardzo skomplikowane. Tymczasem autorzy pokazują, że są one przystępne i da się o nich prosto opowiedzieć każdemu matematycznemu laikowi. Książka jest napisana lekko i z humorem, co zachęca do czytania, ale na powinno się tego robić 'jednym tchem' i 'od deski do deski'. Należy raczej wracać do lektury wielokrotnie, wybierając ulubione rozdziały i delektować się pasjonującą naturą różnych działów matematyki.
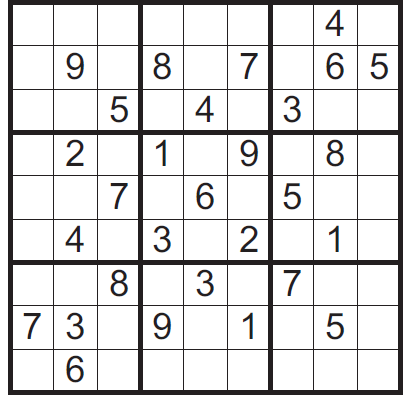
To zabawny samouczek, który zaczynając się niewinnie intrygującą historyjką, krok po kroku, poczynając od najłatwiejszych łamigłówek, prowadzi nas w szpony, nie bójmy się użyć tego słowa, uzależnienia.
