październik 2018

Zad. 1. Niech M będzie środkiem boku AB w trójkącie ABC. Wiedząc, że |∡BAC| + |∡MCB| = 90°, wykaż, że trójkąt jest równoramienny lub prostokątny.

Zad. 2. W trójkącie ABC zachodzi: |∡B| = 22,5° i |∡C| = 45°. Wykaż, że wysokość AH, środkowa BM i dwusieczna CL przecinają się w jednym punkcie.

Zad. 3. Wykaż, że w dowolnym trójkącie na dłuższym boku leży spodek krótszej dwusiecznej.Czy tak samo jest w przypadku wysokości? A w przypadku środkowej?

Zad. 4. (wolna amerykanka) Niech W będzie punktem przecięcia dwusiecznej kąta A z okręgiem opisanym na trójkącie ABC. Wykaż, że |AW| > (|AB| + |AC|)/2.

Wyniki :

Za zadania 1-3 punkty zdobyli:

• 30 pkt. -Jacek Bagiński (nauczyciel matematyki, I LO Kraków), Michel Migas (student matematyki PW), Tadeusz Porzucek (emerytowany nauczyciel, Gostyń), Dominik Sulik (uczeń, I LO Kraków) 
• 22 pkt. - Jakub Węgrecki (student filozofii, UJ)
• 20 pkt. - Dominik Bysiewicz (uczeń, GM Dwujęzyczne w Krośnie), Iwona Gruszecka (nauczycielka matematyki, LO CLV Warszawa )
• W kategorii wolnej amerykanki punkty zdobyli:

• 10 pkt. - Jacek Bagiński, Dominik Bysiewicz, Zygmunt Krawczyk (nauczyciel, SLO Żary), Michel Migas, Tadeusz Porzucek, Dominik Sulik oraz Jakub Węgrecki.

Odpowiedzi:

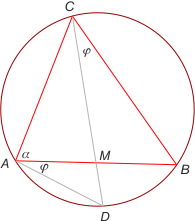
Zad. 1. Niech D będzie punktem przecięcia prostej CM z okręgiem opisanym na trójkącie. Wówczas kąty DAB i DCB są przystające (jako oparte na tym samym łuku). Stąd kąt DAC jest prosty. Oznacza to, że CD jest średnicą okręgu, a tym samym symetralną boku AB (jeśli AB nie jest średnicą). Stąd trójkąt ABC jest równoramienny. Natomiast jeśli AB jest średnicą, to trójkąt jest prostokątny.

Zad. 2. Zauważmy, że L jest punktem przecięcia dwusiecznych kąta ACH oraz kąta zewnętrznego XAH. Oznacza to, że HL jest dwusieczną kąta prostego AHL (zewnętrznego dla trójkąta AHC). Zatem HL jest równoległe do AC. Wysokość AH i dwusieczna CL są przekątnymi trapezu CALH. Wystarczy zatem udowodnić fakt, że prosta przechodząca przez punkt przecięcia przekątnych trapezu i punkt wspólny przedłużeń jego ramion przechodzi także przez środki jego podstaw. Tak jest, bowiem z twierdzenia Talesa mamy (*) ^|AL|/_|LB| = ^|CH|/_|HB|. Niech BM przechodzi przez punkt przecięcia przekątnych trapezu CALH. Wówczas na mocy twierdzenia Cevy mamy (^|AL|/_|LB|)·(^|HB|/_|HC|)·(^|CM|/_|MA|) = 1. Uwzględniając (*) mamy ^|CM|/_|MA| = 1, czyli M jest środkiem AC.

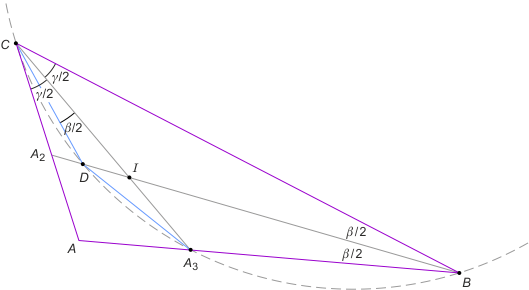
Zad. 3. Niech |AB| > |AC|. Wówczas (*) γ/2 > β/2. Na dwusiecznej BA₂ weźmy punkt D taki, że |∡DCA₃| = β/2. Wówczas punkty D, A₃, B, C są współokręgowe (twierdzenie odwrotne do twierdzenia o kątach wpisanych opartych na przystających łukach). Wobec (*) mamy |∡DCB| > |∡CBA₃|, zatem cięciwa DB jest dłuższa od cięciwy CA₃. Ostatecznie mamy |BA₂|> |BD| > |CA₃|, co kończy dowód.

Analogiczna własność zachodzi dla wysokości, z tym że ich spodek może też wypadać na przedłużeniu boku. Własność ta wynika wprost ze wzoru na pole trójkąta.
Analogiczna własność zachodzi dla środkowych. Wynika ona ze wzoru na długość środkowej m_c = ¹/₂√(2a²+2b²–c²). Jak wyprowadzić ten wzór?

Zad. 4. (wolna amerykanka) Z twierdzenia sinusów mamy |AB| = 2Rsinγ, |AC| = 2Rsinβ oraz |AW| = 2Rsin(β+^α/₂). Wystarczy wykazać, że sinγ + sinβ < sin(β+^α/₂). Mamy sinγ + sinβ = 2sin((γ+β)/2)·cos((γ–β)/2) = 2sin((180°–α)/2)·cos((180°–α–2β)/2) = 2sin(90°–^α/₂)·cos(90°–(α+2β)/2) = 2cos(^α/₂)·sin((α+2β)/2) < sin(β+^α/₂), co kończy dowód.