Zad. 1. W pięciokącie wypukłym wszystkie boki są równe oraz równe są cztery przekątne. Czy ten pięciokąt jest foremny?
Zad. 2. Jaka jest największa możliwa liczba kątów ostrych w wielokącie wypukłym?
Zad. 3. Pole trapezu ABCD wynosi 90. P jest środkiem podstawy AB. Odcinki PC i PD przecinają przekątne trapezu odpowiednio w punktach M i N. Oblicz pole czworokąta ONPM, gdzie O jest punktem przecięcia przekątnych, wiedząc, że jedna z podstaw jest dwa razy dłuższa od drugiej.
Zad. 4. (wolna amerykanka) Wykaż, że dla każdego trójkąta o bokach długości a, b i c prawdziwa jest nierówność a2 + b2 + c2 ≤ 9R2, gdzie R jest promieniem okręgu opisanego na tym trójkącie.
Za zadania 1-3 punkty zdobyli:
-
30 pkt. -Jacek Bagiński (nauczyciel matematyki, I LO Kraków), Dominik Bysiewicz (uczeń, I LO Krosno), Tadeusz Porzucek (emerytowany nauczyciel, Gostyń),
- 28 pkt. - Jakub Węgrecki (student filozofii, UJ), Dominik Sulik (uczeń, I LO Kraków), Iwona Gruszecka (nauczycielka matematyki, CLV LO Warszawa ) i Michel Migas (student, PW).
W kategorii wolnej amerykanki 10 pkt. zdobyli: Jacek Bagiński, Zygmunt Krawczyk (nauczyciel, SLO Żary), Michel Migas, Tadeusz Porzucek, Dominik Sulik oraz Jakub Węgrecki.
Gratulacje!
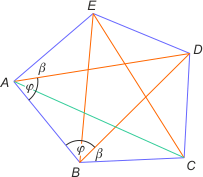
Zad. 1. Niech AC różni się od pozostałych przekątnych. Zauważmy, że trójkąty BCD i AED są przystające na mocy cechy bbb. Stąd kąty EAD i DBC mają takie same miary. Z równoramienności trójkąta ABD mamy przystawanie kątów DAB i ABD. Kąty EAB i ABC są przystające jako sumy kątów o równych miarach. Oznacza to, że trójkąty ABC i AEB są przystające na mocy cechy bkb, skąd |AC| = |EB|. Otrzymaliśmy równość wszystkich przekątnych, boków i kątów wewnętrznych, zatem pięciokąt jest foremny.
Zad. 2. Zauważmy, że suma wszystkich kątów zewnętrznych wielokąta wynosi 360°, więc co najwyżej 3 spośród nich mogą być rozwarte, a tym samym co najwyżej 3 kąty wewnętrzne mogą być ostre.
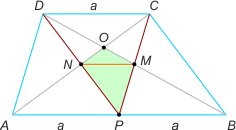
Zad. 3. Zauważmy, że N i M są środkami odcinków PC i PD, bo czworokąty APCD i PBCD są równoległobokami. Pole szukanego czworokąta otrzymamy, odejmując od pola trójkąta ABO pola trójkątów APN i PBM. Pole trapezu S = 3ah/2 = 90, skąd ah = 60. Trójkąty AOB i DOC są podobne w skali 2:1, stąd SAOB = 1/2·2a·2h/3 = 2ah/3=40. Dalej SAPN = 1/2a·h/2 = ah/4= 15 = SPBM. Ostatecznie SNPMO = 40–2·15 = 10.
W drugim przypadku SAOB = 1/2a·h/3 = ah/6 = 10, a SAPN = 1/2·a/2·h/5 = ah/20 = 3 = SPBM, skąd ostatecznie SNPMO = 10–2·3 = 4.
Zad. 4. Zadanie zostało powtórzone (patrz kwiecień 2018). Jest więc okazja, aby przedstawić inne rozwiązanie. Niech M oznacza środek ciężkości trójkąta, a O - środek okręgu na nim opisanego. Skorzystamy z zależności wektorowej OM = OA+OB+OC/9. Wówczas OM2 = (OA2+OB2+OC2+2OA•OB+2OA•OC+2OB•OC)/9. Zauważmy, że AB = OB–OA. Mamy zatem AB2 = (OB–OA)2, skąd 2OA•OB = OA2+OB2–AB2 = 2R2–c2. Ostatecznie otrzymujemy |OM|2 = (R2+R2+R2+2R2–c2+2R2–b2+2R2–a2)/9 = R2 – (a2+b2+c2)/9 ≥ 0, skąd wynika teza.
Czy wiesz, kto z wrocławskich matematyków został uwiecz-niony na tym znakomitym portrecie w piżamie? Kto jest autorem tego obrazu? Gdzie można go obejrzeć?
Jako młody chłopak Knaster ożenił się z poznaną w Paryżu Marią Morską - muzą Skaman-drytów (zm. w 1945 roku). W czasach wrocła-wskich jego drugą żoną była Regina Lewandowska. Pierwszej żonie Knastera poświęcona jest książka Hanny Faryny-Paszkiewicz "Opium życia".
Steinhaus twierdził, że nazwisko Knaster brzmi w dopeł-niaczu Knastra, a sam Knaster upierał się przy formie Knastera. 
